Kunci Jawaban Matematika Kelas 8 Halaman 74, 75

Soal Latihan 2.2

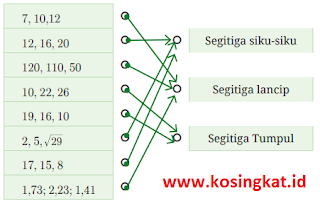
1. Sesuaikan tiga bilangan berikut dengan pasangan yang sesuai apakah termasuk segitiga siku-siku, segitiga lancip, dan segitiga tumpul. 

Jawaban :

2. Buktikan bahwa diantara kelompok tiga bilangan berikut manakah yang merupakan tripel Pythagoras. 

Jawaban :

a. 25² = 625
24² + 17² = 576 + 289 = 865
Jadi, Kelompok tersebut Bukan Triple Pythagoras.

b. 13² = 169
11² + 7²= 121 + 49 = 170
Jadi, Kelompok tersebut Bukan Triple Pythagoras.

c. (13/2)² = 169/4 = 42,25
6² + (5/2)² = 36 + 6 1/4 = 42,25
Jadi, Kelompok tersebut Iya, Triple Pythagoras.

3. Seekor kucing berada di atas genting dan terlihat kebingungan karena tidak bisa turun. Aysha yang melihat kucing tersebut langsung mencari galah dan kemudian diikat dengan keranjang kecil pada ujung galah tersebut. Saat menolong kucing tersebut, Cintia melihat Aysha dan mencoba membantunya untuk mengarahkan galah yang telah diikat keranjang tepat pada titik lokasi kucing pada jarak 4 meter. Jika jarak pandangan Cintia terhadap kucing diperkirakan 5 meter. Tentukan hasil dari pernyataan berikut ini. 

a. Tentukan jarak atap yang ditempati kucing terhadap tanah tempat Aysha berdiri. 

b. Tentukan panjang galah yang digunakan Aysha menolong kucing, jika tinggi Aysha 165 cm. 

Jawaban :

a. Jarak kucing dengan tanah
= √(5² - 4²)
= √(25 - 16)
= √9
= 3
Jadi, jarak kucing dengan tanah adalah 3 m.

b. Tinggi Aysha 165 cm, maka panjang galah adalah
3m - 1,65m = 1,35 m.

4. Kusen jendela yang berbentuk persegi panjang memiliki tinggi 40,8 cm dan panjang 30,6 cm, serta panjang salah satu diagonalnya 52,5 cm. Apakah kusen jendela benar-benar persegi panjang? Jelaskan. 

Jawaban :

(52,5)² = 2756,25
(40,8)² + (30,6)² = 1664,64 + 936,36 = 2601

Karena panjang diagonal kuadrat tidak sama dengan jumlah kuadrat dua sisi lainnya maka kusen Bukan benar-benar persegi panjang.

5. Jika (p - q), p, (p + q) membentuk tripel Pythagoras, 

a. Tentukan hubungan antara p dan q. 

b. Jika p = 12, tentukan tripel Pythagoras.

Jawaban :

a. Berdasarkan gambar di atas, dapat digunakan aturan Teorema Pythagoras yaitu. 
(p - q)² + p² = (p + q)²
p² - 2pq + q² + p² = p² + 2pq + q²
2p² - p² - 2pq - 2pq + q² - q² = 0
p² - 4pq = 0
p(p - 4a) = 0
Maka nilai p adalah p = 0 atau p - 4q = 0, p = 4q
Jadi, hubungan antara p dan q adalah p = 4q.

b. Jika p = 12, menggunakan hubungan poin a, maka nilai q adalah
p = 4q
12 = 4q
q= 12/4
q = 3
Karena p = 12 dan q = 3, Tripel Pythagorasnya adalah
(12 - 3)² + 12² = (12 + 3)²
9² + 12² = 15
Jadi, Tripel Pythagorasnya adalah 9, 12, 15.

Bagikan Artikel ini