Kunci Jawaban Matematika Kelas 8 Halaman 45 - 52 Uji Kompetensi 6

Berikut ini adalah pembahasan dan Kunci Jawaban Matematika Kelas 8 Semester 2 Halaman 45 - 52. Bab 6 Teorema Phytagoras Uji Kompetensi 6 Hal 45 - 52 Nomor 1 - 20 PG dan 1 - 10 Esai. Kunci jawaban ini dibuat untuk membantu mengerjakan soal matematika bagi kelas 8 di semester 2 halaman 45 - 52. Semoga dengan adanya pembahasan serta kunci jawaban uji kompetensi 6 matematika kelas 8, adik-adik kelas 8 dapat menyelesaikan tugas Teorema Phytagoras Kelas 8 Halaman 45 - 52 yang diberikan oleh bapak ibu/guru. Kunci Jawaban MTK Kelas 8 Semester 2.

Kunci Jawaban Matematika Kelas 8 Halaman 45 - 52 Uji Kompetensi 6

Kunci Jawaban Pilihan Ganda Matematika Kelas 8 Halaman 45 - 49

1. D. Jika k² = l² + m² , besar ∠K = 90°

2. A. 10

3. B. (i) dan (iii) 

4. D. (iii) dan (iv)

5. C. 66 satuan 

6. C. 2√13 dm

7. D. Penampungan Hewan dan Kantor polisi

8. A. 10 cm, 24 cm, 26 cm

9. B. 8 cm 

10. B. 56 cm

11. C. 168 cm

12. C. √202 km 

13. C. 276 inci²

14. B. 13√2 cm

15. A. 5

16. A. 5 dm² 

17. A. 25 cm

18. B. 12√2 cm 

19. C. 4√3 cm

20. D. 90√3 cm²

Kunci Jawaban Esai Matematika Kelas 8 Halaman 49 - 52

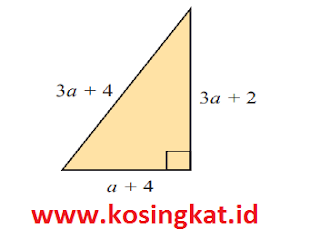
1. Tentukan nilai a pada gambar berikut.

Jawaban :

(a + 4)² + (3a + 2)² = (3a + 4)²
a² + 8a + 16 + 9a² + 12a + 4 = 9a² + 24a + 16
a² – 4a + 4 = 0
(a – 2)² = 0
a – 2 = 0
a = 2
Jadi, nilai a yang memenuhi adalah 2.

2. Tentukan apakah ∆ABC dengan koordinat A(−2, 2) ,B(−1, 6) dan C(3, 5) adalah suatu segitiga siku siku? Jelaskan. 

Jawaban :

AB² = (6 - 2)² + (-1 + 2)² = 16+1 = 17 
AB = √17

AC² = (5 - 2)² + (3 + 2)² = 9 + 25 = 34
AC = √34

BC² = (5 - 6)² + (3 + 1)² = 1 + 16 = 17
BC = √17


AB² + BC² = AC²
(√17)² + √17)² = (√34)²
17 + 17 = 34
34 = 34
Jadi, benar bawha segitiga ABC adalah segitiga Siku-siku.

3. Buktikan bahwa (a² − b² ), 2ab, (a² + b² ) membentuk tripel Pythagoras. 

Jawaban :

(a² – b²)² + (2ab)² = (a² + b²)²
a⁴ – 2a²b² + b⁴ + 4a²b² = a⁴ + 2a²b² + b⁴
a⁴ + 2a²b² + b⁴ = a⁴ + 2a²b² + b⁴
Jadi, Terbukti bahwa (a2 – b2), 2ab, (a2 + b2) membentuk Tripel Pythagoras.

4. Perhatikan gambar di samping. Persegi ABCD mempunyai panjang sisi 1 satuan dan garis AC adalah diagonal.

Jawaban :

a) Hubungannya memiliki ukuran dan bentuk yang sama.

b) m∠ABC = 90°, m∠ACB = 45° dan m∠BAC = 45°

c) AB² + BC² = AC²
1² + 1² = AC²
AC = √2 

d) Pada bagian b tidak ada yang berubah, besar sudutnya tetap sama. Sedangkan pada bagian c panjang diagonalnya berubah menjadi √72 satuan.

5. Tentukan nilai x dari gambar di bawah ini.

Jawaban :

a² + b² = c²
8² + 15² = c²
64 + 225 = c²
289 = c²
c = √289
c = 17

Luas segitiga = 1/2 x alas x tinggi
21/2 x 8 x 15 = 1/2 x 17 x x
8 x 15 = 17 x x
x = 120/17
Jadi, nilai x adalah 120/17.

6. Tentukan keliling segitiga ABC di bawah ini.

Jawaban :

AC / AB = 1 / √3
AC / 8 = 1 / √3
AC = 8/3 √3

BC / AB = 2 / √3
BC / 8 = 2 / √3
BC = 16/3 √3

Keliling = AB + AC + BC
= 8  + (8/3 √3) + (16/3 √3)
= 8 + 8√3 cm
Jadi, keliling segitiga ABC tersebut adalah 8 + 8√3 cm.

7. Sebuah air mancur terletak di tengah perempatan jalan di pusat kota. Mobil merah dan mobil hijau sama-sama melaju meninggalkan air mancur tersebut. 

Jawaban :

a) Tabel jarak

b) Kecepatan mobil hijau = √(jarak tempuh mobil merah² - jarak kedua mobil²) / 2
= √(100² - 80²) / 2
= 60 / 2
= 30 km/jam
Jadi, kecepatan mobil hijau pada saat itu adalah 30 km/jam.

8. Perhatikan gambar segitiga ABC di bawah ini.

Jawaban :

a) Keliling segitiga ACD adalah 24√3 + 24 cm
b) Perbandingan keliling Δ ACD dan Δ ABC adalah 1 : 2
c) Perbandingan luas Δ ACD dan luas Δ ABC adalah 1 : 4

9. Gambar di bawah ini merupakan balok ABCD.EFGH dengan panjang 10 dm, lebar 6 dm, dan tinggi 4 dm.

Jawaban :

Jarak terpendeknya dengan berjalan dari titik P ke titik tengah BF kemudian ke Q maka,

P ke tengah BF = √(PB² + (1/2 x BF)²)
= √((10 / 2)² + (1/2 x 4)²)
= √(5² + 2²)
= √29

tengah BF ke Q = √(BC² + (1/2 x BF)²)
= √((6 / 2)² + (1/2 x 4)²)
= √(3² + 2²)
= √13

Jarak terpendek = √29 + √13 dm
Jadi, jarak terpendek yang mungkin ditempuh oleh laba-laba tersebut adalah √29 + √13 dm.

10. Pada gambar di bawah ini, ketiga sisi sebuah segitiga siku-siku ditempel setengah lingkaran.

Jawaban :

a) Dengan menggunakan rumus luas setengah lingkaran = (πr2)/2 maka didapat,
- Luas setengah lingkaran dengan diameter 3 cm adalah 9π/4 cm²
- Luas setengah lingkaran dengan diameter 4 cm adalah 16π/4 cm²
- Luas setengah lingkaran dengan diameter 5 cm adalah 25π/4 cm²

b) Hubungannya luas setengah lingkaran pada diameter 5 cm sama besarnya dengan jumlah dua setengah lingkaran lainnya.

Bagikan Artikel ini