Kunci Jawaban Matematika Kelas 9 Halaman 307 - 313 Uji Kompetensi 5
Berikut ini adalah pembahasan dan Kunci Jawaban Matematika Kelas 9 Semester 1
Halaman 307 - 313. Bab 5 Bangun Ruang Sisi Lengkung Uji Kompetensi 5 Hal
307 - 313 Nomor 1 - 20 Essai. Kunci jawaban ini dibuat untuk membantu
mengerjakan soal matematika bagi kelas 9 di semester 1 halaman 307 - 313.
Semoga dengan adanya pembahasan serta kunci jawaban ini adik-adik kelas 9
dapat menyelesaikan tugas Bangun Ruang Sisi Lengkung Kelas 9 Halaman 307
- 313 yang diberikan oleh bapak ibu/guru. Kunci Jawaban MTK Kelas 9 Semester
1.
Kunci Jawaban Matematika Kelas 9 Halaman 307 - 313 Uji Kompetensi 5
1. Tentukan luas permukaan tiap-tiap bangun.
Jawaban :
a) Luas = 2 x π x 5 x (5 + 14) = 190π cm²
b) Luas = 2 x π x 12 x (12 + 40) = 1.248π dm²
c) Luas = 2 x π x 1 x (1 + 2) = 6π m²
d) Luas = π x 9 x (9 + 15) = 216π cm²
e) Luas = π x 8 x (8 + 17) = 200π dm²
f) Luas = π x 1 x (1 + 2) = 3π m²
g) Luas = 4 x π x 12 x 12 = 576π cm²
h) Luas = 4 x π x 5 x 5 = 100π m²
i) Luas = 4 x π x 8 x 8 = 256π dm²
j) Luas = 2 x π x 6 x (6 + 9) = 180π m²
k) Luas = π x 6 x (6 + 3√13) = (36 + 18√13)π dm²
l) Luas = 4 x π x 8 x 8 = 256π cm²
a) Luas = 2 x π x 5 x (5 + 14) = 190π cm²
b) Luas = 2 x π x 12 x (12 + 40) = 1.248π dm²
c) Luas = 2 x π x 1 x (1 + 2) = 6π m²
d) Luas = π x 9 x (9 + 15) = 216π cm²
e) Luas = π x 8 x (8 + 17) = 200π dm²
f) Luas = π x 1 x (1 + 2) = 3π m²
g) Luas = 4 x π x 12 x 12 = 576π cm²
h) Luas = 4 x π x 5 x 5 = 100π m²
i) Luas = 4 x π x 8 x 8 = 256π dm²
j) Luas = 2 x π x 6 x (6 + 9) = 180π m²
k) Luas = π x 6 x (6 + 3√13) = (36 + 18√13)π dm²
l) Luas = 4 x π x 8 x 8 = 256π cm²
2. Tentukan volume tiap-tiap bangun.
Jawaban :
a) Volume = π x 5 x 5 x 14 = 350π cm³
b) Volume = π x 12 x 12 x 40 = 5760π dm³
c) Volume = π x 1 x 1 x 2 = 2π m³
d) Volume = 1/3 x π x 9 x 9 x 12 = 324π cm³
e) Volume = 1/3 x π x 8 x 8 x 15 = 320π dm³
f) Volume = 1/3 x π x 1 x 1 x √3 = √3/3π m³
g) Volume = 4/3 x π x 12 x 12 x 12 = 2304π cm³
h) Volume = 4/3 x π x 5 x 5 x 5 =500/3π m³
i) Volume = 4/3 x π x 8 x 8 x 8 = 2048/3π dm³
j) Volume = π x 6 x 6 x 9 = 324π m³
k) Volume = 1/3 x π x 6 x 6 x 9 = 108π dm³
l) Volume = 4/3 x π x 8 x 8 x 8 = 2048/3π cm³
a) Volume = π x 5 x 5 x 14 = 350π cm³
b) Volume = π x 12 x 12 x 40 = 5760π dm³
c) Volume = π x 1 x 1 x 2 = 2π m³
d) Volume = 1/3 x π x 9 x 9 x 12 = 324π cm³
e) Volume = 1/3 x π x 8 x 8 x 15 = 320π dm³
f) Volume = 1/3 x π x 1 x 1 x √3 = √3/3π m³
g) Volume = 4/3 x π x 12 x 12 x 12 = 2304π cm³
h) Volume = 4/3 x π x 5 x 5 x 5 =500/3π m³
i) Volume = 4/3 x π x 8 x 8 x 8 = 2048/3π dm³
j) Volume = π x 6 x 6 x 9 = 324π m³
k) Volume = 1/3 x π x 6 x 6 x 9 = 108π dm³
l) Volume = 4/3 x π x 8 x 8 x 8 = 2048/3π cm³
3. Tentukan rumus luas permukaan bangun-bangun pada tabel di atas.
Jawaban :
a) Setengah tabung = πr(r + t) + 2rt
b) Setengah kerucut =1/2 πr(r + s) + rt
c) Setengah bola = 3πr²
a) Setengah tabung = πr(r + t) + 2rt
b) Setengah kerucut =1/2 πr(r + s) + rt
c) Setengah bola = 3πr²
4. Dari jawaban soal nomor 3 bandingkan dengan rumus bangun-bangun pada
sebelah kiri.
Jawaban :
a) Tidak
b) Jika suatu bangun ruang dibagi menjadi dua bagian yang sama maka luas permukaannya tidak sama dengan setengah kali lipatnya.
a) Tidak
b) Jika suatu bangun ruang dibagi menjadi dua bagian yang sama maka luas permukaannya tidak sama dengan setengah kali lipatnya.
5. Tentukan rumus volume bangun-bangun pada tabel di atas.
Jawaban :
a) Volume setengah tabung = 1/2 πr²t
b) Volume setengah kerucut = = 1/6 πr²t
c) Volume setengah bola = 2/3 πr³
a) Volume setengah tabung = 1/2 πr²t
b) Volume setengah kerucut = = 1/6 πr²t
c) Volume setengah bola = 2/3 πr³
6. Kemudian bandingkan jawabanmu dengan rumus bangun-bangun pada sebelah
kiri.
Jawaban :
a) Ya
b) Jika suatu bangun ruang dibagi menjadi dua bagian yang sama maka volumenya sama dengan setengah kali lipatnya.
a) Ya
b) Jika suatu bangun ruang dibagi menjadi dua bagian yang sama maka volumenya sama dengan setengah kali lipatnya.
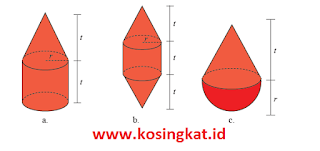
7. Tentukan luas permukaan dan volume tiap-tiap bangun.
Jawaban :
a) Luas = = πr² + 2πrt + πr√(r² + t²) = πr(r + 2t + √(r² + t²))
Volume = πr²t + 1/3πr²t = 4/3πr2t
b) Luas = 2πrt + 2πr√(r² + t²) = 2πr(t + √(r² + t²) )
Volume = πr²t + 2 × 1/3 πr²t = 5/3πr²t
c) Luas = 1/2 × 4πr² + πr √(r² + t²) = πr(2r + √(r² + t²) )
Volume = 1/2 × 4/3 πr³ + 1/3 πr²t = 1/3 πr²(2r + t)
d) Luas = 1/2 × 4πr² + 2πrt + πr² = πr(3r + 2t)
Volume = πr²t + 1/2 × 4/3πr3 = 1/3 πr²(3t + 2r)
e) Luas = 1/2 × 4πr² + 2πrt + πr √(r² + t²) = πr(2r + 2t + √(r² + t²) )
Volume = 1/2 × 4/3 πr3 + πr²t + 1/3 πr²t = 2/3 πr² (r + 2t)
f) Luas = 4πr² + 2πrt = 2πr(2r + t)
Volume = 4/3 πr³ + πr²t = 1/3 πr²(4r + 3t)
a) Luas = = πr² + 2πrt + πr√(r² + t²) = πr(r + 2t + √(r² + t²))
Volume = πr²t + 1/3πr²t = 4/3πr2t
b) Luas = 2πrt + 2πr√(r² + t²) = 2πr(t + √(r² + t²) )
Volume = πr²t + 2 × 1/3 πr²t = 5/3πr²t
c) Luas = 1/2 × 4πr² + πr √(r² + t²) = πr(2r + √(r² + t²) )
Volume = 1/2 × 4/3 πr³ + 1/3 πr²t = 1/3 πr²(2r + t)
d) Luas = 1/2 × 4πr² + 2πrt + πr² = πr(3r + 2t)
Volume = πr²t + 1/2 × 4/3πr3 = 1/3 πr²(3t + 2r)
e) Luas = 1/2 × 4πr² + 2πrt + πr √(r² + t²) = πr(2r + 2t + √(r² + t²) )
Volume = 1/2 × 4/3 πr3 + πr²t + 1/3 πr²t = 2/3 πr² (r + 2t)
f) Luas = 4πr² + 2πrt = 2πr(2r + t)
Volume = 4/3 πr³ + πr²t = 1/3 πr²(4r + 3t)
8. Apakah mungkin T = K? Jika ya, tentukan perbandingan r : t.
Jawaban :
Dengan memasukkan kedalam persamaan T = K maka diperoleh t = 0 atau 4r + 3t = 0, sehingga keduanya Tidak Mungkin.
Dengan memasukkan kedalam persamaan T = K maka diperoleh t = 0 atau 4r + 3t = 0, sehingga keduanya Tidak Mungkin.
9. Apakah mungkin T = B? Jika ya, tentukan perbandingan r : t.
Jawaban :
Dengan memasukkan kedalam persamaan T = B maka diperoleh r = t, sehingga perbandingan r : t adalah 1 : 1.
Dengan memasukkan kedalam persamaan T = B maka diperoleh r = t, sehingga perbandingan r : t adalah 1 : 1.
10. Apakah mungkin K = B? Jika ya, tentukan perbandingan r : t.
Jawaban :
Dengan memasukkan kedalam persamaan K = B maka diperoleh r = 1 dan t = 2√2, sehingga perbandingan r : t adalah 1 : 2√2.
Dengan memasukkan kedalam persamaan K = B maka diperoleh r = 1 dan t = 2√2, sehingga perbandingan r : t adalah 1 : 2√2.
11. Apakah mungkin T = K = B? Kemukakan alasanmu.
Jawaban : Tidak Mungkin, karena dari jawaban no 8, 9, dan 10 menghasilkan jawaban yang berbeda beda.
12. Gambar di samping merupakan cokelat berbentuk kerucut yang dibagi
menjadi empat bagian, A, B, C dan D.
Jawaban :
a) A : B = 87 : 55
b) B : C = 165 : 112
c) C : D = 35 : 9
a) A : B = 87 : 55
b) B : C = 165 : 112
c) C : D = 35 : 9
13. Perhatikan kembali gambar pada Soal nomor 12.
a. Tentukan perbandingan volume A dengan volume B.
b. Tentukan perbandingan volume B dengan volume C.
c. Tentukan perbandingan volume C dengan volume D.
Jawaban :
a) A : B = 37 : 29
b) B : C = 19 : 7
c) C : D = 7 : 1
a) A : B = 37 : 29
b) B : C = 19 : 7
c) C : D = 7 : 1
15. Untuk tiap pasangan bangun ruang yang sebangun, hitung panjang yang
ditanyakan
Jawaban :
a) r = 2 cm
b) s = 15 m
c) Jika L1/L2 = m, maka r1/r2 = t1/t2 = √m
Jika V1/V2 = n, maka r1/r2 = t1/t2 = ³√n
a) r = 2 cm
b) s = 15 m
c) Jika L1/L2 = m, maka r1/r2 = t1/t2 = √m
Jika V1/V2 = n, maka r1/r2 = t1/t2 = ³√n
16. Bola di dalam kerucut. Gambar di samping merupakan suatu kerucut
dengan AB = AC = BC = d.
Jawaban :
r = 2L/k
= 1/2√3d² / 3d
= √3/6d
V = 4/3πr³
= 4/3π (√3/6d)³
= √3/54 πd³
Jadi, volume bola tersebut adalah √3/54 πd³
r = 2L/k
= 1/2√3d² / 3d
= √3/6d
V = 4/3πr³
= 4/3π (√3/6d)³
= √3/54 πd³
Jadi, volume bola tersebut adalah √3/54 πd³
17. Kerucut di dalam bola. Gambar di samping merupakan suatu kerucut
dengan AB = AC = BC = d.
Jawaban :
r = abc / 4L
= (d x d x d) / √3d²
= d/√3
V = 4/3πr³
= 4/3π(d/√3)³
= 4/9√3 πd³
r = abc / 4L
= (d x d x d) / √3d²
= d/√3
V = 4/3πr³
= 4/3π(d/√3)³
= 4/9√3 πd³
18. Budi mengecat tong sebanyak 14 buah. Tong tersebut berbentuk tabung
terbuka dengan jari-jari 50 cm dan tinggi 1 m.
Jawaban :
Luas permukaan tong = πr² + 2πrt
= 22/7(1/2)² + 2(22/7)(1/2)(1)
= 22/7(1/4 + 1)
= 55/14
Banyak cat yang dibutuhkan = luas permukaan tong x banyak tong
= 55/14 x 14
= 55 kaleng cat
Jadi, banyak kaleng cat yang dibutuhkan untuk mengecat semua tong adalah 55 kaleng.
Luas permukaan tong = πr² + 2πrt
= 22/7(1/2)² + 2(22/7)(1/2)(1)
= 22/7(1/4 + 1)
= 55/14
Banyak cat yang dibutuhkan = luas permukaan tong x banyak tong
= 55/14 x 14
= 55 kaleng cat
Jadi, banyak kaleng cat yang dibutuhkan untuk mengecat semua tong adalah 55 kaleng.
19. Gambar di bawah ini merupakan 3 macam desain kolam renang. Skala yang
digunakan adalah 1 : 200.
Jawaban :
a) Lakukan pendekatan untuk menghitung luas desain kolom. Salah satunya dengan membuat kotak-kotak kecil pada masing-masing desain.
b) volume = luas sebenarnya × ketinggian kolam = luas sebenarnya × t
a) Lakukan pendekatan untuk menghitung luas desain kolom. Salah satunya dengan membuat kotak-kotak kecil pada masing-masing desain.
b) volume = luas sebenarnya × ketinggian kolam = luas sebenarnya × t
20. Globe. Globe merupakan tiruan bumi yang berbentuk bola. Terdapat
suatu globe dengan diameter 30 cm. Jika skala pada globe tersebut adalah 1
: 20.000.000, tentukan luas permukaan bumi
Jawaban :
Jari-jari bumi sebenarnya = r x skala
= d/2 x skala
= 30/2 x 20.000.000
= 300.000.000 cm
= 3.000 km
Luas permukaan bumi = 4πr²
= 4 x 3,14 x 3.000 x 3.000
= 113.040.000 km²
Jadi, luas permukaan bumi sebenarnya adalah 113.040.000 km².
Jari-jari bumi sebenarnya = r x skala
= d/2 x skala
= 30/2 x 20.000.000
= 300.000.000 cm
= 3.000 km
Luas permukaan bumi = 4πr²
= 4 x 3,14 x 3.000 x 3.000
= 113.040.000 km²
Jadi, luas permukaan bumi sebenarnya adalah 113.040.000 km².


Belum ada Komentar untuk "Kunci Jawaban Matematika Kelas 9 Halaman 307 - 313 Uji Kompetensi 5"
Posting Komentar