Kunci Jawaban Matematika Kelas 9 Halaman 280 - 283 Latihan 5.1

Berikut ini adalah pembahasan dan Kunci Jawaban Matematika Kelas 9 Semester 1 Halaman 280 - 283. Bab 5 Bangun Ruang Sisi Lengkung Latihan 5.1 Hal 280 - 283 Nomor 1 - 10 Essai. Kunci jawaban ini dibuat untuk membantu mengerjakan soal matematika bagi kelas 9 di semester 1 halaman 280 - 283. Semoga dengan adanya pembahasan serta kunci jawaban ini adik-adik kelas 9 dapat menyelesaikan tugas Bangun Ruang Sisi Lengkung Kelas 9 Halaman 280 - 283 yang diberikan oleh bapak ibu/guru. Kunci Jawaban MTK Kelas 9 Semester 1.

Kunci Jawaban Matematika Kelas 9 Halaman 280 - 283 Latihan 5.1

1. Hitung luas permukaan dan volume dari bangun tabung berikut ini:

Jawaban :

Luas permukaan tabung = (2π x r x r) + (2π x r x t) = 2 x r x (r + t)
Volume tabung = π x r x r x t 

a) Luas = (2π x 4 x 4) + (2π x 4 x 10)
= 32π + 80π 
= 112π cm²
Volume = π x 4 x 4 x 10
= 160π cm³

b) Luas = (2π x 7 x 7) + (2π x 7 x 6)
= 98π + 84π 
= 182π cm²
Volume = π x 7 x 7 x 6
= 294π cm³

c) Luas = (2π x 4 x 4) + (2π x 4 x 12)
= 32π + 96π 
= 128π cm²
Volume = π x 4 x 4 x 12
= 192π cm³

d) Luas = (2π x 1 x 1) + (2π x 1 x 8)
= 2π + 16π 
= 18π m²
Volume = π x 1 x 1 x 8
= 8π m³

e) Luas = (2π x 2 x 2) + (2π x 2 x 10)
= 8π + 40π 
= 48π m²
Volume = π x 2 x 2 x 10
= 40π m³

f ) Luas = (2π x 3,5 x 3,5) + (2π x 3,5 x 20)
= 24,5π + 140π 
= 164,5π cm²
Volume = π x 3,5 x 3,5 x 20
= 245π cm³

2. Tentukan panjang dari unsur tabung yang ditanyakan.

Jawaban :

a) V = π x r x r x t
600π = π x 10 x 10 x t
t = 600π / 100π
t = 6 cm

b) L = 2π x r x (r + t)
120π = 2π x 5 x (5 + t)
5 + t = 120π / 10π
5 + t = 12
t = 7 cm

c) V = π x r x r x t
224π = π x 4 x 4 x t
t = 224π / 16π
t = 14 cm

d) L = 2π x r x (r + t)
528π = 2π x r x (r + 13)
528π = 2π x r² + 13r
r² + 13r - 264 = 0
(r + 24) (r - 11)
r = 11 cm

e) L = 2π x r x (r + t)
450π = 2π x r x (r + 15)
450π = 2π x r² + 15r
r² + 15r - 225 = 0
r = 9 cm

f) V = π x r x r x t
294π = π x r x r x 6 
r² = 294π / 6π
r = √49
r = 7 cm

3. Berpikir Kritis. Terdapat suatu tabung dengan jari-jari r cm dan tinggi tabung t cm, dimana r < t. Misalkan tabung tersebut memiliki volume V cm3 dan luas permukaan L cm2.

Jawaban :

V = L
2πr(r + t) = πr²t
2(r + t) = rt
(r + t) / rt = 1/2
1/r + 1/t = 1/2

Jadi, nilai 1/r + 1/t = 1/2.

4. Tantangan. Gambar di samping merupakan suatu magnet silinder. Alas dari magnet tersebut dibentuk dari dua lingkaran yang sepusat.

Jawaban :

a) Luas permukaan = 2 × luas alas + luas selimut dalam + luas selimut luar
= 2(π(r2)² – π(r1)²) + 2πr1t + 2πr2t
= 2(π(6)² – π(4)²) + 2π(4)(10) + 2π(6)(10)
= 40π + 80π + 120π
= 240π cm²

b) Volume = volume tabung besar – volume tabung kecil
= π(r2)²t – π(r1)²t
= π(6)²(10) – π(4)²(10)
= 200π cm³

5. Irisan Tabung. Misalkan terdapat suatu tabung dengan jari-jari r cm dan panjang t cm.

Jawaban :

Luas irisan = luas permukaan tabung / 2 + luas persegi
= 2 x r x (r + t) / 2 + (2r x t)
= r(r + t) + (2r x t)

6. Tandon Bocor. Terdapat suatu tandon yang berbentuk tabung dengan jari-jari 50 cm tinggi 2 m. Tandon tersebut berisi air sebanyak ¾ dari volume total.

Jawaban :

Vair = 3/4 x π x r x r x t 
= 3/4 x 3,14 x 50 x 50 x 200
= 1.177.500 cm³

Waktu = Vair / Kecepatan
= 1177500 / 50
= 23.550 detik
Jadi, air pada tandong tersebut akan habis setelah 23.550 detik.

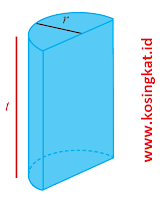
7. Pondasi rumah. Alas dari pondasi rumah pak Ahmad berbentuk seperti gambar di samping. Jika tinggi pondasi adalah 2 m maka:

Jawaban :

a) Luas pondasi = luas persegi - luas lingkaran
= (30 x 30) - (3,14 x 5 x 5)
= 821,5 cm²

b) Volume pondasi = luas pondasi x tinggi
= 821,5 x 200
= 164.300 cm³

8. Analisis Kesalahan. Rudi menghitung volume tabung dengan diameter 5 cm dan tinggi 12 cm. Rudi menghitung

Jawaban : Budi salah menggunakan rumus, seharusnya V = πr²t. Selain itu Budi tertukar ketika mensubstitusikan nilai r dan t.

9. Tabung miring. Pada gambar di bawah terdapat dua buah bangun sisi lengkung. Sebelah kiri merupakan tabung dengan jari-jari r dan tinggi t.

Jawaban :

a) Metodenya adalah dengan membuat tumpukan koin yang membentuk tabung miring.
b) Sama, karena kaidah volume adalah luas alas dikalikan dengan tinggi. Dengan merubah tabung menjadi tabung miring tidak merubah alas dan tingginya, sehingga tidak terjadi perubahan volume.

10. Kaleng susu. Suatu perusahaan susu memiliki kotak susu ukuran 40 cm × 60 cm × 20 cm. Kapasitas maksimal kotak tersebut adalah 48 kaleng susu.

Jawaban :

Misal r = 5 cm, maka t = 20 x (24 / 48) = 10 cm.
Diperoleh luas permukaan kaleng = 2πr(r + t) = 2π(5)(5 + 10) = 150π.

Jadi, luas permukaannya minimal saat r = 5 cm dan t = 10 cm.

Bagikan Artikel ini