Kunci Jawaban Matematika Kelas 9 Halaman 254 - 259 Latihan 4.4
Berikut ini adalah pembahasan dan Kunci Jawaban Matematika Kelas 9 Semester 1
Halaman 254 - 259. Bab 4 Kekongruenan dan Kesebangunan Latihan 4.4 Hal 254 - 259
Nomor 1 - 17 Essai. Kunci jawaban ini dibuat untuk membantu mengerjakan soal
matematika bagi kelas 9 di semester 1 halaman 254 - 259. Semoga dengan adanya
pembahasan serta kunci jawaban ini adik-adik kelas 9 dapat menyelesaikan tugas
Kekongruenan dan Kesebangunan Kelas 9 Halaman 254 - 259 yang diberikan oleh
bapak ibu/guru. Kunci Jawaban MTK Kelas 9 Semester 1.
Kunci Jawaban Matematika Kelas 9 Halaman 254 - 259 Latihan 4.4
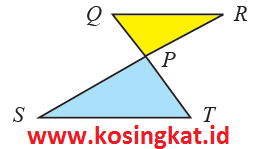
1. Pada gambar di samping, QR//ST.
a. Buktikan bahwa ΔQRP dan ΔTPS sebangun
b. Tuliskan perbandingan sisi-sisi yang bersesuaian.
Jawaban :
a) m∠RQP = m∠STP (berseberangan dalam)
m∠QRP = m∠TSP (berseberangan dalam)
m∠QPR = m∠TPS (bertolak belakang)
Jadi, ΔQRP dan ΔTPS sebangun karena memiliki sudut-sudut yang bersesuaian sama besar.
b) QR/TS = RP/SP = QP/TP
a) m∠RQP = m∠STP (berseberangan dalam)
m∠QRP = m∠TSP (berseberangan dalam)
m∠QPR = m∠TPS (bertolak belakang)
Jadi, ΔQRP dan ΔTPS sebangun karena memiliki sudut-sudut yang bersesuaian sama besar.
b) QR/TS = RP/SP = QP/TP
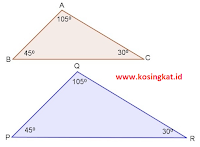
2. Perhatikan gambar berikut.
a. Buktikan bahwa ΔABC dan ΔPQR sebangun.
b. Tuliskan perbandingan sisi-sisi yang bersesuaian.
Jawaban :
a) PQ = √20² - 16²
= √400 - 256
= √144
= 12
AB / PQ = 4/16 = 1/4
m∠BAC = m∠QPR = 90° (diketahui)
Jadi, ΔABC dan ΔPQR sebangun karena memenuhi syarat kesebangunan.
b) AB/PQ = AC/PR = BC/QR
a) PQ = √20² - 16²
= √400 - 256
= √144
= 12
AB / PQ = 4/16 = 1/4
m∠BAC = m∠QPR = 90° (diketahui)
Jadi, ΔABC dan ΔPQR sebangun karena memenuhi syarat kesebangunan.
b) AB/PQ = AC/PR = BC/QR
3. Perhatikan gambar berikut. Apakah ∆KMN sebangun dengan ∆OLN?
Tunjukkan.
Jawaban :
Iya,
m∠LON = m∠MKN (siku-siku)
m∠ONL = m∠KNM (berhimpit)
m∠OLN = m∠KMN (sehadap karena OL //KM)
Jadi, ΔKMN dan ΔOLN sebangun karena sudut-sudut yang bersesuaian sama besar.
Iya,
m∠LON = m∠MKN (siku-siku)
m∠ONL = m∠KNM (berhimpit)
m∠OLN = m∠KMN (sehadap karena OL //KM)
Jadi, ΔKMN dan ΔOLN sebangun karena sudut-sudut yang bersesuaian sama besar.
4. Pada ∆ABC dan ∆PQR diketahui m∠A = 105°, m∠B = 45°, m∠P = 45°, dan m∠Q
= 105°.
Jawaban :
a) Iya, karena dua pasang sudut yang bersesuaian sama besar, yaitu m∠A = m∠Q = 105° dan m∠B = m∠P = 45°.
b) AB dengan QP, BC dengan PR, dan AC dengan QR.
a) Iya, karena dua pasang sudut yang bersesuaian sama besar, yaitu m∠A = m∠Q = 105° dan m∠B = m∠P = 45°.
b) AB dengan QP, BC dengan PR, dan AC dengan QR.
5. Perhatikan gambar. Diketahui m∠ABC = 90°, siku-siku di B.
Jawaban :
a) m∠BAD = m∠CAB (berhimpit)
m∠BDA = m∠CBA = 90° (diketahui siku-siku)
Jadi, ΔADB dan ΔABC sebangun karena memiliki dua pasang sudut yang bersesuaian sama besar.
b) m∠BCD = m∠ACB (berhimpit)
m∠CDB = m∠CBA = 90° (diketahui siku-siku)
Jadi, ΔBDC dan ΔABC sebangun karena memiliki dua pasang sudut yang bersesuaian sama besar.
a) m∠BAD = m∠CAB (berhimpit)
m∠BDA = m∠CBA = 90° (diketahui siku-siku)
Jadi, ΔADB dan ΔABC sebangun karena memiliki dua pasang sudut yang bersesuaian sama besar.
b) m∠BCD = m∠ACB (berhimpit)
m∠CDB = m∠CBA = 90° (diketahui siku-siku)
Jadi, ΔBDC dan ΔABC sebangun karena memiliki dua pasang sudut yang bersesuaian sama besar.
6. Perhatikan gambar.
a. Tunjukkan bahwa ΔFCE ∼ ΔACB.
b. Tunjukkan bahwa ΔFCE ∼ ΔDEB.
c. Tunjukkan bahwa ΔACB ∼ ΔDEB.
d. Tentukan panjang FE dan AF.
Jawaban :
a) ∠ CFE = ∠ CAB (sudut sehadap)
∠ CEF = ∠ CBA (sudut sehadap)
∠ FCE = ∠ ACB (sudut berimpit)
Jadi, ΔFCE sebangun dengan ΔACB.
b) ∠ CFE = ∠ EDB (sudut sehadap)
∠ CEF = ∠ DBE (sudut sehadap)
∠ FCE = ∠ DEB (sudut sehadap)
Jadi, ΔFCE sebangun dengan ΔDEB.
c) ∠ CAB = ∠ BDE (sudut sehadap)
∠ ABC = ∠ DBE (sudut berimpit)
∠ ACB = ∠ DEB (sudut sehadap)
Jadi, ΔACB sebangun dengan ΔDEB.
d) FE = CE x DB / BE
= 5 x 12 / 10
= 6
AF = BE x CF / CE
= 10 x 4 / 5
= 8
Jadi, panjang FE adalah 6 cm dan panjang AF adalah 8 cm.
a) ∠ CFE = ∠ CAB (sudut sehadap)
∠ CEF = ∠ CBA (sudut sehadap)
∠ FCE = ∠ ACB (sudut berimpit)
Jadi, ΔFCE sebangun dengan ΔACB.
b) ∠ CFE = ∠ EDB (sudut sehadap)
∠ CEF = ∠ DBE (sudut sehadap)
∠ FCE = ∠ DEB (sudut sehadap)
Jadi, ΔFCE sebangun dengan ΔDEB.
c) ∠ CAB = ∠ BDE (sudut sehadap)
∠ ABC = ∠ DBE (sudut berimpit)
∠ ACB = ∠ DEB (sudut sehadap)
Jadi, ΔACB sebangun dengan ΔDEB.
d) FE = CE x DB / BE
= 5 x 12 / 10
= 6
AF = BE x CF / CE
= 10 x 4 / 5
= 8
Jadi, panjang FE adalah 6 cm dan panjang AF adalah 8 cm.
7. Perhatikan gambar.
a. Hitunglah panjang EB
b. Hitunglah panjang CE
Jawaban :
a) CE/DE = CB / AB
6/5 = (6 + EB) / 7
6 x 7 = 5 x (6 + EB)
42 = 30 + 5EB
EB = (42 - 30) / 5
EB = 2,4 cm
Jadi, panjang EB adalah 2,4 cm.
b) 4/6 = 8 / (4 + CE)
4 x (4 + CE) = 6 x 8
16 + 4CE = 48
4CE = 48 - 16
CE = 32/4
CE = 8
Jadi, panjang CE adalah 8 cm.
a) CE/DE = CB / AB
6/5 = (6 + EB) / 7
6 x 7 = 5 x (6 + EB)
42 = 30 + 5EB
EB = (42 - 30) / 5
EB = 2,4 cm
Jadi, panjang EB adalah 2,4 cm.
b) 4/6 = 8 / (4 + CE)
4 x (4 + CE) = 6 x 8
16 + 4CE = 48
4CE = 48 - 16
CE = 32/4
CE = 8
Jadi, panjang CE adalah 8 cm.
8. Perhatikan gambar. Hitunglah panjang MN pada gambar di bawah ini.
Jawaban :
MN = (SR x MP + PQ x SM) / SP
= (12 x 3 + 20 x 5) / 8
= (36 + 100) / 8
= 136 / 8
= 17 cm
Jadi, panjang MN adalah 17 cm.
MN = (SR x MP + PQ x SM) / SP
= (12 x 3 + 20 x 5) / 8
= (36 + 100) / 8
= 136 / 8
= 17 cm
Jadi, panjang MN adalah 17 cm.
9. Perhatikan gambar.
Jawaban :
a) ΔABC dengan ΔBDC, ΔABC dengan ΔADB, dan ΔADB dengan ΔBDC.
b) ∆ ABC ∼ ∆ ABD
∠ ABC = ∠ ADB
∠ BAC = ∠ DAB
∠ ACB = ∠ ABD
∆ ABC ∼ ∆ BCD
∠ ABC = ∠ BDC
∠ BAC = ∠ DBC
∠ ACB = ∠ BCD
∆ ABD ∼ ∆BCD
∠ ADB = ∠BDC
∠ DAB = ∠ DBC
∠ ABD = ∠ BCD
c) ∆ ABC ∼ ∆ ABD
AB dengan AD
BC dengan BD
AC dengan BA
∆ ABC ∼ ∆ BCD
AB dengan BD
BC dengan CD
AC dengan BC
∆ ABD ∼ ∆BCD
AD dengan BD
BD dengan CD
AB dengan BC
d) BA = (AC x AD) / BA
BA² = (50 x 32)
BA = √1600
BA = 40 cm
BC = (AB x BD) / AD
BC = (40 x 24) / 32
BC = 960/32
BC = 30 cm
BD = (CD x AD) / BD
BD² = (18 x 32)
BD = √576
BD = 24 cm
a) ΔABC dengan ΔBDC, ΔABC dengan ΔADB, dan ΔADB dengan ΔBDC.
b) ∆ ABC ∼ ∆ ABD
∠ ABC = ∠ ADB
∠ BAC = ∠ DAB
∠ ACB = ∠ ABD
∆ ABC ∼ ∆ BCD
∠ ABC = ∠ BDC
∠ BAC = ∠ DBC
∠ ACB = ∠ BCD
∆ ABD ∼ ∆BCD
∠ ADB = ∠BDC
∠ DAB = ∠ DBC
∠ ABD = ∠ BCD
c) ∆ ABC ∼ ∆ ABD
AB dengan AD
BC dengan BD
AC dengan BA
∆ ABC ∼ ∆ BCD
AB dengan BD
BC dengan CD
AC dengan BC
∆ ABD ∼ ∆BCD
AD dengan BD
BD dengan CD
AB dengan BC
d) BA = (AC x AD) / BA
BA² = (50 x 32)
BA = √1600
BA = 40 cm
BC = (AB x BD) / AD
BC = (40 x 24) / 32
BC = 960/32
BC = 30 cm
BD = (CD x AD) / BD
BD² = (18 x 32)
BD = √576
BD = 24 cm
10. Perhatikan gambar. Diketahui PR = 15 cm dan QU = 2/3 UP. Tentukan
panjang TS.
Jawaban :
PR/UT = QP/QU
15/UT = (2+3) / 2
5 UT = 2 × 15
UT = 30/5
UT = 6 cm
TS = PR - UT
TS = 15 - 6
TS = 9 cm
Jadi, panjang TS adalah 9 cm.
PR/UT = QP/QU
15/UT = (2+3) / 2
5 UT = 2 × 15
UT = 30/5
UT = 6 cm
TS = PR - UT
TS = 15 - 6
TS = 9 cm
Jadi, panjang TS adalah 9 cm.
11. Perhatikan gambar. Diketahui KL = 10 cm dan MN = 14 cm. P dan Q
berturut-turut adalah titik tengah LN dan KM. Tentukan panjang PQ.
Jawaban :
PQ = (MN - KL) / 2
= (14 - 10) / 2
= 4 / 2
= 2 cm
Jadi, panjang PQ adalah 2 cm.
PQ = (MN - KL) / 2
= (14 - 10) / 2
= 4 / 2
= 2 cm
Jadi, panjang PQ adalah 2 cm.
12. Perhatikan gambar.Segitiga ABC adalah segitiga siku-siku sama kaki.
Jika AB = 10 cm dan CD garis bagi sudut C, Tentukan panjang BD.
Jawaban :
Perbandingan sudut 45° (segitiga sama kaki siku-siku) = s : m = 1 : √2
AB : AC = 1 : √2
10/AC = 1/√2
AC = 10√2 cm
BD = AC - EC
BD = (10√2 - 10)
BD = 10 (√2 - 1) cm
Jadi, panjang BD adalah 10 (√2 - 1) cm.
Perbandingan sudut 45° (segitiga sama kaki siku-siku) = s : m = 1 : √2
AB : AC = 1 : √2
10/AC = 1/√2
AC = 10√2 cm
BD = AC - EC
BD = (10√2 - 10)
BD = 10 (√2 - 1) cm
Jadi, panjang BD adalah 10 (√2 - 1) cm.
13. Memperkirakan Tinggi Rumah Pada suatu sore, sebuah rumah dan pohon
yang bersebelahan memiliki panjang bayangan berturut-turut 10 m dan 4
m.
Jawaban :
Tinggi rumah / tinggi pohon = bayangan rumah / bayangan pohon
Tinggi rumah = (10/4) x 10
= 100/4
= 25 m
Jadi, tinggi rumah sebenarnya adalah 25 m.
Tinggi rumah / tinggi pohon = bayangan rumah / bayangan pohon
Tinggi rumah = (10/4) x 10
= 100/4
= 25 m
Jadi, tinggi rumah sebenarnya adalah 25 m.
14. Memperkirakan Tinggi Pohon Untuk menentukan tinggi sebuah pohon,
Ahmad menempatkan cermin di atastanah (di titik E) seperti gambar di bawah
ini.
Jawaban :
AB / CD = BE / ED
AB / 1,4 = 18 /2,1
AB = 1,4 × 18 / 2,1
AB = 12 m
Jadi, perkiraan tinggi pohon tersebut adalah 12 m.
AB / CD = BE / ED
AB / 1,4 = 18 /2,1
AB = 1,4 × 18 / 2,1
AB = 12 m
Jadi, perkiraan tinggi pohon tersebut adalah 12 m.
15. Memperkirakan Tinggi Bukit Dua mahasisiwa Teknik Sipil Agung dan Ali
ingin memperkirakan tinggi suatu bukit terhadap posisinya berdiri yang
tidak jauh dari bukit itu.
Jawaban :
sisi miring segitiga = √4² + 3² = 5
sisi miring segitiga / sisi miring bukit = tinggi segitiga / tinggi bukit
5 / (1540 + 5) = 3 / tinggi bukit
tinggi bukit = (1545 x 3) / 5
= 4635 / 5
= 927 m
Jadi, perkiraan tinggi bukit tersebut adalah 927 m.
sisi miring segitiga = √4² + 3² = 5
sisi miring segitiga / sisi miring bukit = tinggi segitiga / tinggi bukit
5 / (1540 + 5) = 3 / tinggi bukit
tinggi bukit = (1545 x 3) / 5
= 4635 / 5
= 927 m
Jadi, perkiraan tinggi bukit tersebut adalah 927 m.
16. Analisis Kesalahan Gambar (a) menunjukkan persegi dengan panjang sisi
8 satuan.
Jawaban :
Tidak, karena 8 x 8 adalah 64 sedangkan 5 x 13 adalah 65.
Letak kesalahannya terletak pada kemiringan. Bangun A memiliki kemiringan 3/8 sedangkan bangun B memiliki kemiringan 5/13.
Tidak, karena 8 x 8 adalah 64 sedangkan 5 x 13 adalah 65.
Letak kesalahannya terletak pada kemiringan. Bangun A memiliki kemiringan 3/8 sedangkan bangun B memiliki kemiringan 5/13.
17. Analisis Kesalahan Perhatikan gambar di bawah ini! Jelaskan di
manakah letak kesalahannya?
Jawaban : Letak kesalahan terdapat pada luas segitiga merah.
Belum ada Komentar untuk "Kunci Jawaban Matematika Kelas 9 Halaman 254 - 259 Latihan 4.4"
Posting Komentar