Kunci Jawaban Matematika Kelas 8 Halaman 239 - 244 Uji Kompetensi 5
Berikut ini adalah pembahasan dan Kunci Jawaban Matematika Kelas 8 Semester 1 Halaman 239 - 244. Bab 5 Sistem Persamaan Linear Dua Variabel Uji Kompetensi 5 Hal 239 - 244 Nomor 1 - 20 PG dan 1 - 10 Essai. Kunci jawaban ini dibuat untuk membantu mengerjakan soal matematika bagi kelas 8 di semester 1 halaman 239 - 244. Semoga dengan adanya pembahasan serta kunci jawaban ini adik-adik kelas 8 dapat menyelesaikan tugas Sistem Persamaan Linear Dua Variabel Kelas 8 Halaman 239 - 244 yang diberikan oleh bapak ibu/guru. Kunci Jawaban MTK Kelas 8 Semester 1.
Kunci Jawaban Matematika Kelas 8 Halaman 239 - 244 Uji Kompetensi 5
Kunci Jawaban Pilihan Ganda Matematika kelas 8 Halaman 239 - 242
1. A. {(0, 4), (1, 2), (2, 0)}
2. B. (2, −1)
3. D. 4
4. C. (2, −3)
5. B. (−1, 2)
6. A. (1, 5)
7. D. x = 1, y = 1/2
8. B. Rp60.000,00
9. C. 20 tahun
10. A. 25
11. B. Rp1.600,00
12. D. 3
13. C. 56 cm2
14. B. 6
15. A. (−1, 2)
16. D. Tak hingga selesaian
17. A. (1, 3)
18. A. Tidak punya
19. D. 2x + 2y = 62 , x + 4y = 70
20. D. 6 tahun
Kunci Jawaban Essai Matematika kelas 8 Halaman 242 - 244
1. Lengkapi pasangan berurutan untuk tiap-tiap persamaan berikut.
2. Diberikan sistem persamaan linear dua variabel 3x - y = 10 , x - 2y = 0. Tentukan selesaian dari sistem persamaan linear dua variabel di atas.
3. Bioskop dan Tiket Masuk
Malam ini sebuah film animasi terbaru sedang diputar di sebuah bioskop. Beberapa orang dewasa dan anak-anak sedang mengantri membeli tiket.
4. Keliling sebuah persegi panjang 76 dm. Jika selisih antara panjang dan lebar persegi panjang tersebut 10 dm, tentukanlah:
5. Harga 5 buku dan 3 penggaris adalah Rp21.000,00. Jika Maher membeli 4 buku dan 2 penggaris, maka ia harus membayar Rp16.000,00.
6. Jumlah uang Diana dan uang Demi Rp220.000,00. Jika uang Diana ditambah dengan tiga kali lipat uang Demi sama dengan Rp420.000,00, tentukanlah:
7. Jumlah umur Gino dan umur Handoko adalah 60 tahun dan selisih umur mereka adalah 4 tahun (Gino lebih tua). Tentukanlah:
8. Selesaikan sistem persamaan linear dua variabel berikut ini.
9. Perhatikan gambar berikut. Tentukan nilai x dan y
10. Gambar di samping menunjukkan suatu persegi yang dibagi menjadi 6 bagian yang sama. Setiap bagian berupa persegi panjang mempunyai keliling 70 cm. Tentukan luas persegi yang dimaksud.
Jawaban :
a) y = −x + 6; (9, ...)
y = -9 + 6 = -3
(9 , -3)
b) y = 6x − 7; (2, ...)
y = 6(2) - 7 = 12 - 7 = 5
(2 , 5)
c) 2x – 15y = 13, (..., -3/4)
2x - 15(-3/4) = 13
2x = 13 - 45/4 = 7/4
x = 7/4 x 1/2 = 7/8
(7/8 , -3/4)
d) –x + 12y = 7, (..., 3/4)
-x + 12(3/4) = 7
x = 9 - 7 = 2
(2 , 3/4)
a) y = −x + 6; (9, ...)
y = -9 + 6 = -3
(9 , -3)
b) y = 6x − 7; (2, ...)
y = 6(2) - 7 = 12 - 7 = 5
(2 , 5)
c) 2x – 15y = 13, (..., -3/4)
2x - 15(-3/4) = 13
2x = 13 - 45/4 = 7/4
x = 7/4 x 1/2 = 7/8
(7/8 , -3/4)
d) –x + 12y = 7, (..., 3/4)
-x + 12(3/4) = 7
x = 9 - 7 = 2
(2 , 3/4)
2. Diberikan sistem persamaan linear dua variabel 3x - y = 10 , x - 2y = 0. Tentukan selesaian dari sistem persamaan linear dua variabel di atas.
Jawaban :
3x - y = 10 , x - 2y = 0
3x - y = 10 , x = 2y
3(2y) - y = 10
5y = 10
y = 2
x = 2y = 4
Jadi, selesaian dari persamaan linear dua variabel di atas adalah (4 , 2).
3x - y = 10 , x - 2y = 0
3x - y = 10 , x = 2y
3(2y) - y = 10
5y = 10
y = 2
x = 2y = 4
Jadi, selesaian dari persamaan linear dua variabel di atas adalah (4 , 2).
3. Bioskop dan Tiket Masuk
Malam ini sebuah film animasi terbaru sedang diputar di sebuah bioskop. Beberapa orang dewasa dan anak-anak sedang mengantri membeli tiket.
Jawaban :
Misal dewasa = d dan anak-anak = a
a) 2d + 2a = 140.000
d + 3a = 130.000
3d + 5a = ..... ?
d = 130.000 - 3a
2(130.000 - 3a) + 2a = 140.000
260.000 - 6a + 2a = 140.000
4a = 120.000
a = 30.000
d = 130.000 - 3a = 130.000 - 3(30.000) = 40.000
3d + 5a = 3(40.000) + 5(30.000)
= 120.000 + 150.000
= 270.000
Jadi, pada gambar ketiga petugas penjualan akan menagih biaya tiket sebesar 270.000 rupiah.
b) Rp.30.000 (anak-anak)
Misal dewasa = d dan anak-anak = a
a) 2d + 2a = 140.000
d + 3a = 130.000
3d + 5a = ..... ?
d = 130.000 - 3a
2(130.000 - 3a) + 2a = 140.000
260.000 - 6a + 2a = 140.000
4a = 120.000
a = 30.000
d = 130.000 - 3a = 130.000 - 3(30.000) = 40.000
3d + 5a = 3(40.000) + 5(30.000)
= 120.000 + 150.000
= 270.000
Jadi, pada gambar ketiga petugas penjualan akan menagih biaya tiket sebesar 270.000 rupiah.
b) Rp.30.000 (anak-anak)
4. Keliling sebuah persegi panjang 76 dm. Jika selisih antara panjang dan lebar persegi panjang tersebut 10 dm, tentukanlah:
Jawaban :
Misal keliling = k, panjang = p, dan lebar = l
a) 2 x (p + l) = k
2 x (p + l) = 76
p + l = 38
p - l = 10
b) p = 38 - l
(38 - l) - l = 10
38 - 2l = 10
2l = 28
l = 14
p = 38 - l = 38 - 14 = 24
Jadi, panjang dan lebar persegi panjang tersebut adalah panjang = 24 dm, dan lebar = 14 dm.
c) Luas = panjang x lebar
= 24 x 14
= 336 dm2
Jadi, luas persegi panjang tersebut adalah 336 dm2.
Misal keliling = k, panjang = p, dan lebar = l
a) 2 x (p + l) = k
2 x (p + l) = 76
p + l = 38
p - l = 10
b) p = 38 - l
(38 - l) - l = 10
38 - 2l = 10
2l = 28
l = 14
p = 38 - l = 38 - 14 = 24
Jadi, panjang dan lebar persegi panjang tersebut adalah panjang = 24 dm, dan lebar = 14 dm.
c) Luas = panjang x lebar
= 24 x 14
= 336 dm2
Jadi, luas persegi panjang tersebut adalah 336 dm2.
5. Harga 5 buku dan 3 penggaris adalah Rp21.000,00. Jika Maher membeli 4 buku dan 2 penggaris, maka ia harus membayar Rp16.000,00.
Jawaban :
Misal buku = b, dan penggaris = p
5b + 3p = 21.000
4b + 2p = 16.000
______________ -
b + p = 5.000
b = 5.000 - p
5(5.000 - p) + 3p = 21.000
25.000 - 5p + 3p = 21.000
2p = 4.000
p = 2.000
b = 5.000 - p
= 5.000 - 2.000
= 3.000
Yang dibeli suci,
10b + 3p = 10(3.000) + 3(2.000)
= 30.000 + 6.000
= 36.000
Jadi, uang yang harus dibayar oleh suci iyalah Rp36.000,00
Misal buku = b, dan penggaris = p
5b + 3p = 21.000
4b + 2p = 16.000
______________ -
b + p = 5.000
b = 5.000 - p
5(5.000 - p) + 3p = 21.000
25.000 - 5p + 3p = 21.000
2p = 4.000
p = 2.000
b = 5.000 - p
= 5.000 - 2.000
= 3.000
Yang dibeli suci,
10b + 3p = 10(3.000) + 3(2.000)
= 30.000 + 6.000
= 36.000
Jadi, uang yang harus dibayar oleh suci iyalah Rp36.000,00
6. Jumlah uang Diana dan uang Demi Rp220.000,00. Jika uang Diana ditambah dengan tiga kali lipat uang Demi sama dengan Rp420.000,00, tentukanlah:
Jawaban :
Misal Diana = x, dan Demi = y
a) x + y = 220.000
x + 3y = 420.000
b) x = 220.000 - y
(220.000 -y) + 3y = 420.000
220.000 + 2y = 420.000
y =100.000
x = 220.000 - y = 220.000 - 100.000 = 120.000
Jadi, besar uang masing-masing adalah Diana 120.000 dan Demi 100.000.
c) Diana - Demi = 120.000 - 100.000 = 20.000
Jadi, selisih uang Diana dan Demi adalah Rp20.000,00.
Misal Diana = x, dan Demi = y
a) x + y = 220.000
x + 3y = 420.000
b) x = 220.000 - y
(220.000 -y) + 3y = 420.000
220.000 + 2y = 420.000
y =100.000
x = 220.000 - y = 220.000 - 100.000 = 120.000
Jadi, besar uang masing-masing adalah Diana 120.000 dan Demi 100.000.
c) Diana - Demi = 120.000 - 100.000 = 20.000
Jadi, selisih uang Diana dan Demi adalah Rp20.000,00.
7. Jumlah umur Gino dan umur Handoko adalah 60 tahun dan selisih umur mereka adalah 4 tahun (Gino lebih tua). Tentukanlah:
Jawaban :
Misal Gino = g dan Handoko = h
a) g + h = 60
g - h = 4
b) g = 60 - h
(60 - h) - h = 4
60 - 2h = -4
2h = 56
h = 28
g = 60 - h = 60 - 28 = 32
Jadi, umur Gino = 32 dan umur Handoko = 28.
c) Perbandingan umur Gino dan Handoko
G : H = 32 / 28
= 8 / 7
Jadi, perbandingan umur Gino dengan umur Handoko adalah 8 banding 7.
Misal Gino = g dan Handoko = h
a) g + h = 60
g - h = 4
b) g = 60 - h
(60 - h) - h = 4
60 - 2h = -4
2h = 56
h = 28
g = 60 - h = 60 - 28 = 32
Jadi, umur Gino = 32 dan umur Handoko = 28.
c) Perbandingan umur Gino dan Handoko
G : H = 32 / 28
= 8 / 7
Jadi, perbandingan umur Gino dengan umur Handoko adalah 8 banding 7.
8. Selesaikan sistem persamaan linear dua variabel berikut ini.
Jawaban :
a) y = −x + 3
y = −x + 5
-x + 3 = -x + 5
x - x = 5 - 3
0 = 2
Karena tidak sama maka, Sistem persamaan terebut Tidak Memiliki Penyelesaian.
b) x = 2y + 10
2x + 3y = −1
2(2y + 10) + 3y = -1
4y + 20 + 3y = -1
7y = -21
y = -3
x = 2(-3) + 10 = 4
(4 , -3)
c) x + y = 3
x − y = −3
x = 3 - y
(3 - y) - y = -3
3 - 2y = -3
2y = 6
y = 3
x = 3 - 3 = 0
(0 , 3)
d) 2x − 4y = 10
−12x + 24y = −60
(x, y) untuk x dan y semua anggota himpunan bilangan real.
a) y = −x + 3
y = −x + 5
-x + 3 = -x + 5
x - x = 5 - 3
0 = 2
Karena tidak sama maka, Sistem persamaan terebut Tidak Memiliki Penyelesaian.
b) x = 2y + 10
2x + 3y = −1
2(2y + 10) + 3y = -1
4y + 20 + 3y = -1
7y = -21
y = -3
x = 2(-3) + 10 = 4
(4 , -3)
c) x + y = 3
x − y = −3
x = 3 - y
(3 - y) - y = -3
3 - 2y = -3
2y = 6
y = 3
x = 3 - 3 = 0
(0 , 3)
d) 2x − 4y = 10
−12x + 24y = −60
(x, y) untuk x dan y semua anggota himpunan bilangan real.
9. Perhatikan gambar berikut. Tentukan nilai x dan y
Jawaban :
x + 3y = 7
x = 7 - 3y (persamaan 1)
2x + y = 9 (persamaan 2)
2(7 - 3y) + y = 9
14 - 6y + y = 9
5y = 5
y = 1
x = 7 - 3y = 7 - 3(1) = 4
Jadi, nilai x dan y adalah x = 4 dan y = 1.
x + 3y = 7
x = 7 - 3y (persamaan 1)
2x + y = 9 (persamaan 2)
2(7 - 3y) + y = 9
14 - 6y + y = 9
5y = 5
y = 1
x = 7 - 3y = 7 - 3(1) = 4
Jadi, nilai x dan y adalah x = 4 dan y = 1.
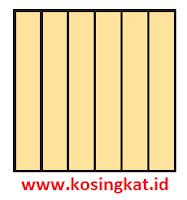
10. Gambar di samping menunjukkan suatu persegi yang dibagi menjadi 6 bagian yang sama. Setiap bagian berupa persegi panjang mempunyai keliling 70 cm. Tentukan luas persegi yang dimaksud.
Jawaban :
Misal lebar = x dan tinggi = y
keliling = 2(x + y)
2(x + y) = 70
y = 6x
2(x + 6x) = 70
14x = 70
x = 5
y = 6x = 30
Luas persegi tersebut = y x y
= 30 x 30
= 900 cm2
Jadi, luas persegi yang dimaksud adalah 900 cm2.
Misal lebar = x dan tinggi = y
keliling = 2(x + y)
2(x + y) = 70
y = 6x
2(x + 6x) = 70
14x = 70
x = 5
y = 6x = 30
Luas persegi tersebut = y x y
= 30 x 30
= 900 cm2
Jadi, luas persegi yang dimaksud adalah 900 cm2.

1 Komentar untuk "Kunci Jawaban Matematika Kelas 8 Halaman 239 - 244 Uji Kompetensi 5"
Maaf mau ngasih masukan, besok lagi yang pilihan ganda dikasih caranya. Terima kasih
Posting Komentar