Kunci Jawaban Matematika Kelas 8 Halaman 167 - 169 Ayo Kita Berlatih 4.4

Berikut ini adalah pembahasan dan Kunci Jawaban Matematika Kelas 8 Semester 1 Halaman 167 - 169. Bab 4 Persamaan Garis Lurus Ayo Kita berlatih 4.4 Hal 167 - 169 Nomor 1 - 10 Essai. Kunci jawaban ini dibuat untuk membantu mengerjakan soal matematika bagi kelas 8 di semester 1 halaman 167 - 169 . Semoga dengan adanya pembahasan serta kunci jawaban ini adik-adik kelas 8 dapat menyelesaikan tugas Persamaan Garis Lurus Kelas 8 Halaman 167 - 169 yang diberikan oleh bapak ibu/guru. Kunci Jawaban MTK Kelas 8 Semester 1.

Kunci Jawaban Matematika Kelas 8 Halaman 167 - 169 Ayo Kita Berlatih 4.4

1. Tulislah persamaan garis yang ditunjukkan tiap-tiap gambar berikut.

Jawaban :

a) Kemiringan (m) = 1/2, melewati titik  (0,-1)
y - y1 = m (x - x1)
y - (-1) = 1/2 (x - 0)
y + 1 = x/2
2y + 2 = x
x - 2y - 2 = 0
Jadi, persamaan garisnya adalah x - 2y - 2 = 0.

b) Kemiringan (m) = -1, melewati titik (0,3)
y - y1 = m (x - x1)
y - 3 = -1 (x - 0)
y - 3 = -x
x + y - 3 = 0
Jadi, persamaan garisnya adalah x + y -3 = 0.

2. Tulislah persamaan garis yang ditunjukkan tiap-tiap gambar berikut.

Jawaban :

a) Kemiringan (m) = 3/5, melewati titik (5,9)
y - y1 = m (x - x1)
y - 9 = 3/5 (x - 5)
y - 9 = 3/5x -3
y - 6 = 3/5x
3/5x - y + 6 = 0
3x - 5y + 30 = 0
Jadi, persamaan garisnya adalah 3x - 5y + 30 = 0.

b) Kemiringan (m) = -1/2, melewati titik (6,3)
y - y1 = m (x - x1)
y - 3 = -1/2 (x - 6)
y - 3 = -1/2x + 3
y - 6 = -1/2x
2y - 12 = -x
x + 2y - 12 = 0
Jadi, persmaan garisnya adalah x + 2y -12 = 0.

3. Tulislah persamaan garis yang ditunjukkan tiap-tiap gambar berikut.

Jawaban :

a) – 10x + 3y = 28 
b) – 8x + 7y = 29

4. Tentukan persamaan garis lurus jika diketahui informasi berikut ini.

Jawaban :

a) x + 3y - 12 = 0
b) 4x + y -2 = 0
c) x + 3y -19 = 0
d) y -x -1 = 0
e) y = 1
f) x = 7
g) 2y -5x -12 = 0

5. Tentukan persamaan garis yang melalui (7, 2) dan sejajar dengan garis 2x − 5y = 8.

Jawaban : 2x -5y - 4 = 0

6. Tentukan persamaan garis yang tegak lurus 2y + 2 = −7/4 (x − 7) dan melalui titik (−2, −3).

Jawaban : 4x -7y -13 = 0

7. Tentukan persamaan garis lurus untuk tiap-tiap garis berikut.

Jawaban :

Jawaban a - d lihat pada gambar berikut.

e) Gradien garis l = 1, karena tegak lurus garis 1 maka gradien garis tersebut adalah
m = -1/gradien l
= -1/1
= -1
c = y - m(x)
= 6 - (-1)(-1)
= 5
Jadi, persamaannya adalah y = -x + 5.

f ) Gradien garis k = -3, karena sejajar garis k maka gradien garis tersebut adalah
m = k
= -3
 c = y - m(x)
= 0 - (-3)(7)
= 21
Jadi, persamaannya adalah y = -3x + 21 

g) Gradien garis n = -0,14, karena sejajar garis n maka gradien garis tersebut adalah
m = gradien n
= -0,14
c = y - m(x)
= 0 - (-0,14)(0)
= 0
Jadi, persamaannya adalah y = -0,14x.

h) Gradien garis m = 2, karena tegak lurus garis m maka gradien garis tersebut adalah
m = -1/gradien m
= -1/2
c = y - m(x)
= -3 - (-1/2)(-3)
= -4,5
Jadi, persamaannya adalah y = -1/2x - 4,5.

8. P berkoordinat di (8, 3), Q berkoordinat di (4, 6), dan O adalah titik asal.

Jawaban :

a) Kemiringan OQ = m = y1/x1 = 6/4 = 3/2
y - y1 = m(x - x1)
y - 3 = 3/2(x - 8)
2y - 6 = 3(x - 8)
2y - 6 = 3x - 24
3x - 2y - 24 + 6 = 0
3x - 2y - 18 = 0
Jadi, persaman garis yang melalui P dan memiliki kemiringn sama dengan garis OQ adalah 3x - 2y - 18 = 0.

b). Garis tersebut melalui (k,1), maka nilai k adalah
3x - 2y - 18 = 0
3(k) - 2(1) - 18 = 0
3k - 2 - 18 = 0
3k -20 = 0
3k = 20
k = 20/3
Jadi, nilai k adalah 20/3.

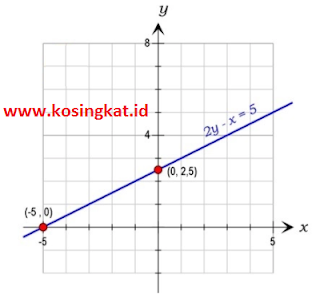
9. Persamaan garis l adalah 2y – x = 5. Tentukan:

Jawaban :

a) (– 5, 0)
b) (0, 5/2)
c) m = 1/2
d)

10. Garis k melalui titik A(−2, 3) dan B(3, 1). Garis l melalui titik C(−6, 5), D(−2, d), T(t , −5). Garis k tegak lurus garis l. Tentukan nilai d dan t.

Jawaban : d = 15 dan t = –10

Bagikan Artikel ini