Kunci Jawaban Matematika Kelas 8 Halaman 67 - 71 Ayo Kita Berlatih 7.1
Berikut ini adalah pembahasan dan Kunci Jawaban Matematika Kelas 8 Semester 2 Halaman 67 - 71. Bab 7 Lingkaran Ayo Kita berlatih 7.1 Hal 67 - 71 Nomor 1 - 2 PG dan 1 - 16 Esai. Kunci jawaban ini dibuat untuk membantu mengerjakan soal matematika bagi kelas 8 di semester 2 halaman 67 - 71. Semoga dengan adanya pembahasan serta kunci jawaban ini adik-adik kelas 8 dapat menyelesaikan tugas Lingkaran Kelas 8 Halaman 67 - 71 yang diberikan oleh bapak ibu/guru. Kunci Jawaban MTK Kelas 8 Semester 2.
2. Diketahui pada suatu lingkaran terdapat empat busur, yaitu busur AB , CD, EF , dan GH. Panjang AB > panjang CD > panjang EF > panjang GH.
Esai
1. Tentukan jari-jari lingkaran yang diketahui diameternya 13 cm.
2. Apakah perpotongan dua diameter selalu di titik pusat?
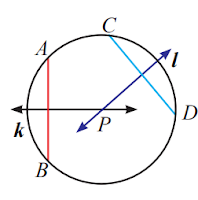
3. Perhatikan gambar di samping. Garis k adalah garis sumbu tali busur AB. Garis l adalah garis sumbu tali busur CD. Titik P adalah perpotongan garis sumbu k dan l. Benarkah perpotongan kedua garis sumbu tersebut tepat di titik pusat? Jelaskan.
4. Adakah tali busur yang lebih panjang dari diameter? Jelaskan.
5. Apakah panjang apotema bisa lebih dari jari-jari? Jelaskan.
6. Dua atau lebih lingkaran dikatakan konsentris jika berpusat di satu titik yang sama. Sebutkan minimal 3 benda (atau bagian benda) yang memuat hubungan konsentris.
7. Diketahui 3 titik berbeda A, B, dan C tidak segaris. Buatlah lingkaran yang melalui 3 titik tersebut.
8. Diketahui 3 titik berbeda A, B, dan C tidak segaris. Buatlah juring setengah lingkaran yang melalui 3 titik tersebut.
9. Komentari pernyataan berikut dengan tanggapan “kadang-kadang”, “selalu”, atau “tidak pernah”.
10. Berdasarkan gambar di samping, tentukan:
a. m∠CGB; b. m∠BGE; c. m∠AGD; d. m∠DGE.
11. Berdasarkan gambar di samping, tentukan: a. m∠ZXV, b. m∠YXW, c. m∠ZXY, d. m∠VXW
12. File Musik Perhatikan tabel berikut. Suatu survei dilakukan secara online untuk mendapatkan informasi tentang banyak file musik yang dimiliki dan didapatkan melalui free download.
13. Tali busur AC dan FD berjarak sama terhadap pusat G. Jika diameter dari lingkaran tersebut adalah 52 cm, maka tentukan panjang AC dan DE.
14. Perhatikan dua argumentasi berikut, kemudian tentukan argumen yang salah menurutmu
15. Perhatikan gambar berikut. Pada gambar di samping, panjang AB = 12 cm dan AC = 16 cm. Titik O merupakan titik pusat lingkaran. Hitunglah:
a. jari-jari lingkaran O,
b. luas daerah yang diarsir.
16. Rumah Makan Pak Anas Pak Anas memiliki suatu rumah makan di suatu daerah di Surabaya. Berikut ini denah rumah makan Pak Anas.
Kunci Jawaban Matematika Kelas 8 Halaman 67 - 71 Ayo Kita Berlatih 7.1
Pilihan Ganda
1. Suatu lingkaran mempunyai jari-jari 10 cm. Pada lingkaran tersebut terdapat tali busur AB, CD, EF, dan GH, dengan panjang berturutturut 10 cm, 12 cm, 14 cm, dan 16 cm.
Jawaban :
A. AB
A. AB
2. Diketahui pada suatu lingkaran terdapat empat busur, yaitu busur AB , CD, EF , dan GH. Panjang AB > panjang CD > panjang EF > panjang GH.
Jawaban :
D. GH
D. GH
Esai
1. Tentukan jari-jari lingkaran yang diketahui diameternya 13 cm.
Jawaban :
r = 1/2 x d
r = 1/2 x 13
r = 13/2
r = 6,5 cm
Jadi, jari-jari lingkaran tersebut adalah 6,5 cm.
r = 1/2 x d
r = 1/2 x 13
r = 13/2
r = 6,5 cm
Jadi, jari-jari lingkaran tersebut adalah 6,5 cm.
2. Apakah perpotongan dua diameter selalu di titik pusat?
Jawaban :
Ya
Ya
3. Perhatikan gambar di samping. Garis k adalah garis sumbu tali busur AB. Garis l adalah garis sumbu tali busur CD. Titik P adalah perpotongan garis sumbu k dan l. Benarkah perpotongan kedua garis sumbu tersebut tepat di titik pusat? Jelaskan.
Jawaban :
Ya, kedua sumbu tersebut adalah garis yang berhimpit dengan diameter lingkaran, sehingga perpotongannya tepat di titik pusat.
Ya, kedua sumbu tersebut adalah garis yang berhimpit dengan diameter lingkaran, sehingga perpotongannya tepat di titik pusat.
4. Adakah tali busur yang lebih panjang dari diameter? Jelaskan.
Jawaban :
Tidak ada, karena diameter adalah tali busur terpanjang.
Tidak ada, karena diameter adalah tali busur terpanjang.
5. Apakah panjang apotema bisa lebih dari jari-jari? Jelaskan.
Jawaban :
Tidak bisa, karena apotema adalah ruas terpendek yang menghubungkan antara titik pusat dengan tali busur, sehingga pasti berada di dalam lingkaran yang artinya panjang apotema tidak mungkin lebih panjang dari jari-jari.
Tidak bisa, karena apotema adalah ruas terpendek yang menghubungkan antara titik pusat dengan tali busur, sehingga pasti berada di dalam lingkaran yang artinya panjang apotema tidak mungkin lebih panjang dari jari-jari.
6. Dua atau lebih lingkaran dikatakan konsentris jika berpusat di satu titik yang sama. Sebutkan minimal 3 benda (atau bagian benda) yang memuat hubungan konsentris.
Jawaban :
- Veleg sepeda dengan ban
- Bingkai jam dinding berbentuk lingkaran
- Sisi dalam dan luar ban sepeda
- Veleg sepeda dengan ban
- Bingkai jam dinding berbentuk lingkaran
- Sisi dalam dan luar ban sepeda
7. Diketahui 3 titik berbeda A, B, dan C tidak segaris. Buatlah lingkaran yang melalui 3 titik tersebut.
Jawaban :
Cara menggambarnya :
- hubungkan titik A ke B, dan B ke C dengan garis lurus
- lukis garis sumbu di kedua garis tersebut
- lukis lingkaran dengan pusat O, di titik hasil persilangan perpanjangan garis sumbu
Cara menggambarnya :
- hubungkan titik A ke B, dan B ke C dengan garis lurus
- lukis garis sumbu di kedua garis tersebut
- lukis lingkaran dengan pusat O, di titik hasil persilangan perpanjangan garis sumbu
8. Diketahui 3 titik berbeda A, B, dan C tidak segaris. Buatlah juring setengah lingkaran yang melalui 3 titik tersebut.
Jawaban :
Langkahnya sama seperti membuat lingkaran, namun panjangnya hanya setengah saja.
Langkahnya sama seperti membuat lingkaran, namun panjangnya hanya setengah saja.
Jawaban :
a. Selalu
b. Selalu
c. Tidak pernah
d. Selalu
a. Selalu
b. Selalu
c. Tidak pernah
d. Selalu
10. Berdasarkan gambar di samping, tentukan:
a. m∠CGB; b. m∠BGE; c. m∠AGD; d. m∠DGE.
Jawaban :
a) m∠CGB = 180° - m∠CGA
= 180° - 60°
= 120°
b) m∠BGE; = 180° - m∠CGB
= 180° - 120°
= 60°
c) m∠AGD = besar sudut siku-siku
= 90°
d) m∠DGE; = 180° - m∠AGC - m∠AGD
= 180° - 60° - 90°
= 30°
a) m∠CGB = 180° - m∠CGA
= 180° - 60°
= 120°
b) m∠BGE; = 180° - m∠CGB
= 180° - 120°
= 60°
c) m∠AGD = besar sudut siku-siku
= 90°
d) m∠DGE; = 180° - m∠AGC - m∠AGD
= 180° - 60° - 90°
= 30°
11. Berdasarkan gambar di samping, tentukan: a. m∠ZXV, b. m∠YXW, c. m∠ZXY, d. m∠VXW
Jawaban :
4x° + 15° = 2x° + 65°
4x° - 2x° = 65° - 15°
2x° = 50°
x° = 50° / 2
x° = 25°
a)
m∠ZXV = 2x° + 65°
= (2 x 25°) + 65°
= 50° + 65°
= 115°
b)
m∠YXW = 4x° + 15°
= (4 x 25°) + 15°
= 100° + 15°
= 115°
c)
m∠ZXY = 180° - m∠YXW
= 180° - 115°
= 65°
d)
m∠VXW = 180° - m∠ZXV
= 180° - 115°
= 65°
4x° + 15° = 2x° + 65°
4x° - 2x° = 65° - 15°
2x° = 50°
x° = 50° / 2
x° = 25°
a)
m∠ZXV = 2x° + 65°
= (2 x 25°) + 65°
= 50° + 65°
= 115°
b)
m∠YXW = 4x° + 15°
= (4 x 25°) + 15°
= 100° + 15°
= 115°
c)
m∠ZXY = 180° - m∠YXW
= 180° - 115°
= 65°
d)
m∠VXW = 180° - m∠ZXV
= 180° - 115°
= 65°
12. File Musik Perhatikan tabel berikut. Suatu survei dilakukan secara online untuk mendapatkan informasi tentang banyak file musik yang dimiliki dan didapatkan melalui free download.
Jawaban :
a)
Sudut pusat 100 files or less = 360° x 76%
= 273,6°
Sudut pusat 101 files to 500 files = 360° x 16%
= 57,6°
Sudut pusat 501 files to 1000 files = 360° x 5%
=18°
Sudut pusat more than 1000 files = 360° x 3%
=10,8°
b) Ukuran juringnya dikira-kira saja disesuaikan dengan gambar C.
c)
a)
Sudut pusat 100 files or less = 360° x 76%
= 273,6°
Sudut pusat 101 files to 500 files = 360° x 16%
= 57,6°
Sudut pusat 501 files to 1000 files = 360° x 5%
=18°
Sudut pusat more than 1000 files = 360° x 3%
=10,8°
b) Ukuran juringnya dikira-kira saja disesuaikan dengan gambar C.
c)
Jawaban :
DE = √(DG2 - EG2)
= √(262 - 102)
= √(676 - 100)
= √576
= 24 cm
AC = 2 x DE
= 2 x 24 cm
= 48 cm
Jadi, panjang AC dan DE adalah 48 cm dan 24 cm.
DE = √(DG2 - EG2)
= √(262 - 102)
= √(676 - 100)
= √576
= 24 cm
AC = 2 x DE
= 2 x 24 cm
= 48 cm
Jadi, panjang AC dan DE adalah 48 cm dan 24 cm.
Jawaban :
Argumen yang benar adalah argumen milik Rusda, karena meskipun garis DG tegak lurus dengan garis BC, namun garis DG bukan diameter lingkaran maka garis DG tidak dapat dikatakan sebagai garis sumbu dari garis BC.
Argumen yang benar adalah argumen milik Rusda, karena meskipun garis DG tegak lurus dengan garis BC, namun garis DG bukan diameter lingkaran maka garis DG tidak dapat dikatakan sebagai garis sumbu dari garis BC.
15. Perhatikan gambar berikut. Pada gambar di samping, panjang AB = 12 cm dan AC = 16 cm. Titik O merupakan titik pusat lingkaran. Hitunglah:
a. jari-jari lingkaran O,
b. luas daerah yang diarsir.
Jawaban :
a)
CB = √(CA2 + AB2)
= √(162 - 122)
= √(256 + 144)
= √400
= 20 cm
Jari-jari lingkaran = 1/2 x CB
= 1/2 x 20
= 10 cm
Jadi, jari-jari lingkaran O adalah 10 cm.
b)
Luas daerah diarsir = (1/2 x lingkaran) - luas segitiga ABC
= (1/2 x π x r x r) - (1/2 x CA x AB)
= (1/2 x 3,14 x 10 x 10) - (1/2 x 16 x 12)
= 157 - 96
= 61 cm2
Jadi, luas daerah yang diarsir adalah 61 cm2.
a)
CB = √(CA2 + AB2)
= √(162 - 122)
= √(256 + 144)
= √400
= 20 cm
Jari-jari lingkaran = 1/2 x CB
= 1/2 x 20
= 10 cm
Jadi, jari-jari lingkaran O adalah 10 cm.
b)
Luas daerah diarsir = (1/2 x lingkaran) - luas segitiga ABC
= (1/2 x π x r x r) - (1/2 x CA x AB)
= (1/2 x 3,14 x 10 x 10) - (1/2 x 16 x 12)
= 157 - 96
= 61 cm2
Jadi, luas daerah yang diarsir adalah 61 cm2.
16. Rumah Makan Pak Anas Pak Anas memiliki suatu rumah makan di suatu daerah di Surabaya. Berikut ini denah rumah makan Pak Anas.
Jawaban :
Panjang = 1,5 m
Lebar = 1,5 m
Kita lihat maksimal tatanan panjang yang dapat dibentuk :
1,5 + 0,5 + 1,5 ≤ 3,5
3,5 ≤ 3,5
Untuk panjang hanya bisa memuat 2 tatanan meja
Kita lihat maksimal tatanan lebar yang dapat dibentuk :
1,5 + 0,5 + 1,5 + 0,5 ≤ 4
4 ≤ 4
Untuk lebarnya hanya bisa memuat 2 tatanan meja
Jadi, jumlah tatanan meja yang bisa dibentuk adalah 4 tatanan meja.
Panjang = 1,5 m
Lebar = 1,5 m
Kita lihat maksimal tatanan panjang yang dapat dibentuk :
1,5 + 0,5 + 1,5 ≤ 3,5
3,5 ≤ 3,5
Untuk panjang hanya bisa memuat 2 tatanan meja
Kita lihat maksimal tatanan lebar yang dapat dibentuk :
1,5 + 0,5 + 1,5 + 0,5 ≤ 4
4 ≤ 4
Untuk lebarnya hanya bisa memuat 2 tatanan meja
Jadi, jumlah tatanan meja yang bisa dibentuk adalah 4 tatanan meja.





Belum ada Komentar untuk "Kunci Jawaban Matematika Kelas 8 Halaman 67 - 71 Ayo Kita Berlatih 7.1"
Posting Komentar