Kunci Jawaban Matematika Kelas 8 Halaman 311 - 321 Uji Kompetensi Semester 2
Berikut ini adalah pembahasan dan Kunci Jawaban Matematika Kelas 8 Semester 2 Halaman 311 - 321. Bab 10 Peluang Uji Kompetensi Semester 2 Hal 311 - 321 Nomor 1 - 25 PG dan 1 - 5 Esai. Kunci jawaban ini dibuat untuk membantu mengerjakan soal matematika bagi kelas 8 di semester 2 halaman 311 - 321. Semoga dengan adanya pembahasan serta kunci jawaban uji kompetensi semester 2 matematika kelas 8, adik-adik kelas 8 dapat menyelesaikan tugas Peluang Kelas 8 Halaman 311 - 321 yang diberikan oleh bapak ibu/guru. Kunci Jawaban MTK Kelas 8 Semester 2.
2. Amati gambar di samping. Tentukan keliling dan luas daerah yang diarsir. (π = 3,14)
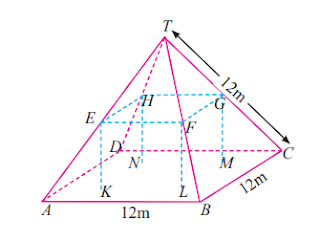
3. Dalam model ini, lantai loteng ABCD berbentuk persegi. Tiang yang menopang atap merupakan rusuk balok EFGH.KLMN. Titik E terletak di tengah AT, titik F di tengah BT, titik G di tengah CT, dan titik H di tengah DT. Semua rusuk piramid pada model tersebut panjangnya 12 m.
a. Hitunglah luas lantai loteng ABCD.
b. Hitunglah panjang EF
4. Kecepatan mobil balap Grafik berikut menunjukkan kecepatan mobil balap sepanjang lintasan 3 km selama putaran kedua.
5. Ketika berjalan-jalan di sebuah mall, Gunarso mendapatkan keberuntungan sebagai pengunjung mall terpilih pada hari itu. Gunarso berkesempatan memilih 1 hadiah dari 3 kotak yang sudah disediakan panitia mall. Setiap kotak tersebut berisi bola berwarna merah mewakili mobil, kuning mewakili motor, dan hijau mewakili TV dengan komposisi sebagai berikut.
Kunci Jawaban Matematika Kelas 8 Halaman 311 - 321 Uji Kompetensi Semester 2
Kunci Jawaban Pilihan Ganda Uji Kompetensi Semester 2 Matematika Kelas 8 Halaman 311
1. A. 12
2. B. 11 meter
3. A. 150
4. D. 72√3 cm2
5. A. 32√2 cm2
6. B. 100
7. D. 42
8. C. 80°
9. D. 41
10. B. 7 cm dan 5 cm
11. B. 3 buah D. 5 buah
12. B. 792 cm dan 1.140 cm3
13. A
14. B. 10 cm
15. C. 12 cm
16. C. 77
17. D. 90
18. C. 18
19. B. 175
20. C. 1.350
21. B. 3/4
22. B. 8
23. D. 3/7
24. A. 5/36
25. D. Erik
Kunci Jawaban Esai Uji Kompetensi Semester 2 Matematika Kelas 8 Halaman 319
1. Keliling Segitiga Berdasarkan gambar, segitiga ABC adalah segitiga siku-siku, dengan sudut siku-siku di B. Panjang BD = 6 m dan panjang AB = 8 m.
Jika luas segitiga ADC 50% lebih besar dari luas segitiga ABD, tentukan keliling segitiga ADC.
Jawaban :
AD = √(AB2 + BD2)
AD = √(82 + 62)
AD = √(64 + 36)
AD = √100
AD = 10 m
Luas ABC = Luas ABD + Luas ADC
= Luas ABD + (3/2 x Luas ABD)
= (1/2 x AB x BD) + (1/2 x 3/2 x AB x BD)
= (1/2 x 8 x 6) + (1/2 x 3/2 x 8 x 6)
= 24 + 36
= 60 m2
Luas ABC = 1/2 x AB x BC
60 = 1/2 x 8 x BC
BC = 60 x 2 / 8
BC = 120 / 8
BC = 15 m
DC = BC - BD
DC = 15 - 6
DC = 9 m
AC = √(AB2 + BC2)
AC = √(82 + 152)
AC = √(64 + 225)
AC = √289
AC = 17 m
Keliling ADC = AD + DC + AC
= 10 + 9 + 17
= 36 m
Jadi, keliling segitiga ADC 36 m.
AD = √(AB2 + BD2)
AD = √(82 + 62)
AD = √(64 + 36)
AD = √100
AD = 10 m
Luas ABC = Luas ABD + Luas ADC
= Luas ABD + (3/2 x Luas ABD)
= (1/2 x AB x BD) + (1/2 x 3/2 x AB x BD)
= (1/2 x 8 x 6) + (1/2 x 3/2 x 8 x 6)
= 24 + 36
= 60 m2
Luas ABC = 1/2 x AB x BC
60 = 1/2 x 8 x BC
BC = 60 x 2 / 8
BC = 120 / 8
BC = 15 m
DC = BC - BD
DC = 15 - 6
DC = 9 m
AC = √(AB2 + BC2)
AC = √(82 + 152)
AC = √(64 + 225)
AC = √289
AC = 17 m
Keliling ADC = AD + DC + AC
= 10 + 9 + 17
= 36 m
Jadi, keliling segitiga ADC 36 m.
2. Amati gambar di samping. Tentukan keliling dan luas daerah yang diarsir. (π = 3,14)
Jawaban :
jari-jari lingkaran = 5 cm
panjang sisi persegi = 10 cm
Keliling persegi tersebut = 10 + 10 + 5 + 5 = 30 cm
Keliling lingkaran tersebut = (1/2 keliling lingkaran ) + 5 + 5
= (1/2 x π x 2 x r) + 10
= (1/2 x 3,14 x 2 x 5) + 10
= 15,7 + 10
= 25,7 cm
Keliling daerah yang diarsir = keliling persegi + keliling lingkaran
= 30 + 25,7
= 55,7 cm
Luas persegi diarsir = sisi x sisi
= 10 x 10
= 100 cm2
Luas lingkaran diarsir = 1/2 x luas lingkaran
= 1/2 x π x r x π
= 1/2 x 3,14 x 5 x 5
= 39,25 cm2
Luas daerah yang diarsir seluruhnya = luas persegi + luas lingkaran
= 100 + 39,25
= 139,25 cm2
Jadi, keliling daerah yang diarsir tersebut adalah 55,7 cm dan luas daerah yang diarsir tersebut adalah 139,25 cm2.
jari-jari lingkaran = 5 cm
panjang sisi persegi = 10 cm
Keliling persegi tersebut = 10 + 10 + 5 + 5 = 30 cm
Keliling lingkaran tersebut = (1/2 keliling lingkaran ) + 5 + 5
= (1/2 x π x 2 x r) + 10
= (1/2 x 3,14 x 2 x 5) + 10
= 15,7 + 10
= 25,7 cm
Keliling daerah yang diarsir = keliling persegi + keliling lingkaran
= 30 + 25,7
= 55,7 cm
Luas persegi diarsir = sisi x sisi
= 10 x 10
= 100 cm2
Luas lingkaran diarsir = 1/2 x luas lingkaran
= 1/2 x π x r x π
= 1/2 x 3,14 x 5 x 5
= 39,25 cm2
Luas daerah yang diarsir seluruhnya = luas persegi + luas lingkaran
= 100 + 39,25
= 139,25 cm2
Jadi, keliling daerah yang diarsir tersebut adalah 55,7 cm dan luas daerah yang diarsir tersebut adalah 139,25 cm2.
3. Dalam model ini, lantai loteng ABCD berbentuk persegi. Tiang yang menopang atap merupakan rusuk balok EFGH.KLMN. Titik E terletak di tengah AT, titik F di tengah BT, titik G di tengah CT, dan titik H di tengah DT. Semua rusuk piramid pada model tersebut panjangnya 12 m.
b. Hitunglah panjang EF
Jawaban :
a)
Luas lantai loteng ABCD = AB x BC
= 12 x 12
= 144 cm2
Jadi, luas lantai loteng ABCD adalah 144 cm2.
b)
Perhatikan gambar tersebut letak EF tepat di tengah-tengah antar puncak T dengan Alas ABCD, selain itu segitga ABT juga sebangun dengan segitiga EFT. Sehingga panjang EF akan 1/2 x panjang AB.
EF = 1/2 x AB
EF = 1/2 x 12
EF = 6 m
Jadi, panjang EF adalah 6 m.
a)
Luas lantai loteng ABCD = AB x BC
= 12 x 12
= 144 cm2
Jadi, luas lantai loteng ABCD adalah 144 cm2.
b)
Perhatikan gambar tersebut letak EF tepat di tengah-tengah antar puncak T dengan Alas ABCD, selain itu segitga ABT juga sebangun dengan segitiga EFT. Sehingga panjang EF akan 1/2 x panjang AB.
EF = 1/2 x AB
EF = 1/2 x 12
EF = 6 m
Jadi, panjang EF adalah 6 m.
4. Kecepatan mobil balap Grafik berikut menunjukkan kecepatan mobil balap sepanjang lintasan 3 km selama putaran kedua.
Jawaban :
A) B. 1,5 km
B) C. Sekitar 1,3 km
C) Kecepatan mobil berkurang
A) B. 1,5 km
B) C. Sekitar 1,3 km
C) Kecepatan mobil berkurang
5. Ketika berjalan-jalan di sebuah mall, Gunarso mendapatkan keberuntungan sebagai pengunjung mall terpilih pada hari itu. Gunarso berkesempatan memilih 1 hadiah dari 3 kotak yang sudah disediakan panitia mall. Setiap kotak tersebut berisi bola berwarna merah mewakili mobil, kuning mewakili motor, dan hijau mewakili TV dengan komposisi sebagai berikut.
Jawaban :
Peluang Mobil kotak A)
Peluang Mobil = merah / (merah+kuning+hijau)
= 7 / (7 + 9 + 10)
= 7 / 26
= 0,269
Peluang Mobil kotak B)
Peluang Mobil = merah / (merah+kuning+hijau)
= 8 / (8 + 12 + 8)
= 8 / 28
= 0,285
Peluang Mobil kotak C)
Peluang Mobil = merah / (merah+kuning+hijau)
= 9 / (9 + 12 + 9)
= 9 / 30
= 0,300
Jadi, kota yang memiliki peluang mendapatkan mobil terbesar adalah Kotak C.
Peluang Mobil kotak A)
Peluang Mobil = merah / (merah+kuning+hijau)
= 7 / (7 + 9 + 10)
= 7 / 26
= 0,269
Peluang Mobil kotak B)
Peluang Mobil = merah / (merah+kuning+hijau)
= 8 / (8 + 12 + 8)
= 8 / 28
= 0,285
Peluang Mobil kotak C)
Peluang Mobil = merah / (merah+kuning+hijau)
= 9 / (9 + 12 + 9)
= 9 / 30
= 0,300
Jadi, kota yang memiliki peluang mendapatkan mobil terbesar adalah Kotak C.
Belum ada Komentar untuk "Kunci Jawaban Matematika Kelas 8 Halaman 311 - 321 Uji Kompetensi Semester 2"
Posting Komentar