Kunci Jawaban Matematika Kelas 8 Halaman 12,13 Ayo Kita Berlatih 6.1
Berikut ini adalah pembahasan dan Kunci Jawaban Matematika Kelas 8 Semester 2 Halaman 12,13. Bab 6 Teorema Pythagoras Ayo Kita berlatih 6.1 Hal 12,13 Nomor 6 - 10 Essai. Kunci jawaban ini dibuat untuk membantu mengerjakan soal matematika bagi kelas 8 di semester 2 halaman 12,13. Semoga dengan adanya pembahasan serta kunci jawaban ini adik-adik kelas 8 dapat menyelesaikan tugas Teorema Pythagoras Kelas 8 Halaman 12,13 yang diberikan oleh bapak ibu/guru. Kunci Jawaban MTK Kelas 8 Semester 2.
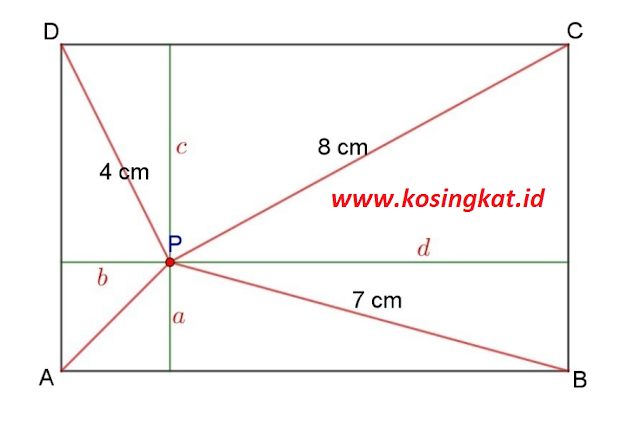
7. Diketahui persegi panjang ABCD dan P merupakan titik di dalam persegi panjang. Jika PC = 8 cm, PD = 4 cm, dan PB = 7 cm, maka PA adalah ..
8. Seorang yang bernama Bhaskara menyusun sebuah persegi dan empat buah segitiga siku-siku yang memiliki panjang sisi yang sama yaitu a, b dan c kedalam sebuah persegi yang mempunyai panjang sisi c.
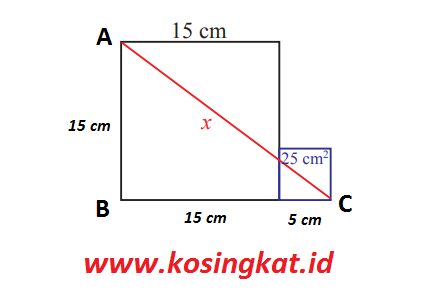
9. Perhatikan gambar dua persegi di samping. Panjang sisi persegi besar adalah 15 cm. Luas persegi kecil adalah 25 cm2 . Tentukan nilai x.
10. Perhatikan gambar di samping. Diketahui ∆ABC siku-siku di B dengan panjang AC = 40 cm dan BC = 24 cm. Titik D terletak pada AB sedemikian sehingga CD = 25 cm. Panjang AD = ... cm.
Terima kasih telah mengunjungi KoSingkat untuk mengakes kunci jawaban matematika kelas 8 halaman 12, 13 semester 2 ayo kita berlatih 6.1. Semoga kunci jawaban dan pembahasan yang diberikan berguna bagi adik-adik dalam mengerjakan tugas yang diberikan.
Kunci Jawaban Matematika Kelas 8 Halaman 12,13 Ayo Kita Berlatih 6.1
6. Tentukan panjang AB dari gambar berikut.
Jawaban :
*Perhatikan Ilustrasi Gambar diatas*
a)
AB = √(CD² + (AD - BC)²)
= √(4² + (4 - 3)²)
= √(16 + 1)
= √17 cm
Jadi, panjang AB adalah √17 cm.
b)
BD = √(BC² + CD²)
= √(7² + 4² BD²)
= √(49 + 16)
= √65
AB² = √(BD² - AD²)
= √((√65)² - 6²)
= √(65 - 36)
= √29 cm
Jadi, panjang AB adalah √29 cm.
c)
AB = √(AO² + BO²)
= √(4² + 5²)
= √(16 + 25)
= √41 cm
Jadi, panjang AB adalah √41 cm.
a)
AB = √(CD² + (AD - BC)²)
= √(4² + (4 - 3)²)
= √(16 + 1)
= √17 cm
Jadi, panjang AB adalah √17 cm.
b)
BD = √(BC² + CD²)
= √(7² + 4² BD²)
= √(49 + 16)
= √65
AB² = √(BD² - AD²)
= √((√65)² - 6²)
= √(65 - 36)
= √29 cm
Jadi, panjang AB adalah √29 cm.
c)
AB = √(AO² + BO²)
= √(4² + 5²)
= √(16 + 25)
= √41 cm
Jadi, panjang AB adalah √41 cm.
7. Diketahui persegi panjang ABCD dan P merupakan titik di dalam persegi panjang. Jika PC = 8 cm, PD = 4 cm, dan PB = 7 cm, maka PA adalah ..
Jawaban :
*Perhatikan ilustrasi gambar diatas*
PA = √(PD² + PB² - PC²)
= √(4² + 7² - 8²)
= √(16 + 49 - 64)
= √(65 - 64)
= √1
= 1 cm
Jadi, panjang PA adalah 1 cm.
PA = √(PD² + PB² - PC²)
= √(4² + 7² - 8²)
= √(16 + 49 - 64)
= √(65 - 64)
= √1
= 1 cm
Jadi, panjang PA adalah 1 cm.
8. Seorang yang bernama Bhaskara menyusun sebuah persegi dan empat buah segitiga siku-siku yang memiliki panjang sisi yang sama yaitu a, b dan c kedalam sebuah persegi yang mempunyai panjang sisi c.
Jawaban :
a) Kelima potongan bangun datar tersebut akan membentuk bangun yang paling kanan seperti pada gambar dibawah ini.
a) Kelima potongan bangun datar tersebut akan membentuk bangun yang paling kanan seperti pada gambar dibawah ini.
b)
Pada gambar (i) terlihat bahwa Luas persegi besar adalah c2.
Dengan menggunakan penjumlahan luas beberapa bangun pada gambar (ii), sehingga akan terbukti bahwa c2 = a2 + b2.
Luas bangun (ii) adalah
2 × (ab) + (b – a)2 = 2ab + b2 –2ab + a2 = a2 + b2
Jadi, karena luas bagun pada gambar (i) sama dengan luas bangun (ii), maka terbukti benar bahwa teorema Pythagoras berlaku.
9. Perhatikan gambar dua persegi di samping. Panjang sisi persegi besar adalah 15 cm. Luas persegi kecil adalah 25 cm2 . Tentukan nilai x.
Jawaban :
*Perhatikan ilustrasi gambar diatas*
Karena kedua bangun tersebut merupakan persegi maka memiliki panjang sisi yang sama.
Panjang sisi bangun (i) = 15 cm
Panjang sisi bangun (ii) = √25 = 5 cm
Sehingga akan diperloeh,
AB = 15 cm
BC = 15 + 5 = 20 cm
Dengan menggunakan pythagoras kita dapat menemukan nilai x.
x = √(AB2 + BC2)
= √(152 + 202)
= √(225 + 400)
= √625
Karena kedua bangun tersebut merupakan persegi maka memiliki panjang sisi yang sama.
Panjang sisi bangun (i) = 15 cm
Panjang sisi bangun (ii) = √25 = 5 cm
Sehingga akan diperloeh,
AB = 15 cm
BC = 15 + 5 = 20 cm
Dengan menggunakan pythagoras kita dapat menemukan nilai x.
x = √(AB2 + BC2)
= √(152 + 202)
= √(225 + 400)
= √625
= 25 cm
Jadi, nilai x adalah 25 cm.
10. Perhatikan gambar di samping. Diketahui ∆ABC siku-siku di B dengan panjang AC = 40 cm dan BC = 24 cm. Titik D terletak pada AB sedemikian sehingga CD = 25 cm. Panjang AD = ... cm.
Jawaban :
AC = 40 cm
BC = 24 cm
CD = 25 cm
AD = AB - DB
Langkah 1 Cari panjang AB :
AB = √(AC2 - BC2)
= √(402 + 242)
= √(1600 - 576)
= √1024
AC = 40 cm
BC = 24 cm
CD = 25 cm
AD = AB - DB
Langkah 1 Cari panjang AB :
AB = √(AC2 - BC2)
= √(402 + 242)
= √(1600 - 576)
= √1024
= 32 cm
Langkah 2 Cari panjang DB :
DB = √(CD2 - BC2)
= √(252 - 242)
= √(625 - 576)
= √49
Langkah 2 Cari panjang DB :
DB = √(CD2 - BC2)
= √(252 - 242)
= √(625 - 576)
= √49
= 7 cm
AD = AB - DB
= 32 - 7
= 25 cm
Jadi, panjang AD adalah 25 cm.
AD = AB - DB
= 32 - 7
= 25 cm
Jadi, panjang AD adalah 25 cm.
Terima kasih telah mengunjungi KoSingkat untuk mengakes kunci jawaban matematika kelas 8 halaman 12, 13 semester 2 ayo kita berlatih 6.1. Semoga kunci jawaban dan pembahasan yang diberikan berguna bagi adik-adik dalam mengerjakan tugas yang diberikan.
Belum ada Komentar untuk "Kunci Jawaban Matematika Kelas 8 Halaman 12,13 Ayo Kita Berlatih 6.1"
Posting Komentar