Kunci Jawaban Matematika Kelas 8 Halaman 113 - 120 Uji Kompetensi 7
Berikut ini adalah pembahasan dan Kunci Jawaban Matematika Kelas 8 Semester 2 Halaman 113 - 120. Bab 7 Lingkaran Uji Kompetensi 7 Hal 113 - 120 Nomor 1 - 20 PG dan 1 - 10 Esai. Kunci jawaban ini dibuat untuk membantu mengerjakan soal matematika bagi kelas 8 di semester 2 halaman 113 - 120. Semoga dengan adanya pembahasan serta kunci jawaban uji kompetensi 7 matematika kelas 8, adik-adik kelas 8 dapat menyelesaikan tugas Lingkaran Kelas 8 Halaman 113 - 120 yang diberikan oleh bapak ibu/guru. Kunci Jawaban MTK Kelas 8 Semester 2.
2. Tentukan keliling daerah yang diarsir pada bangun berikut.
3. Amati gambar di bawah ini. Tentukan keliling dan luas daerah yang diarsir.
4. Perhatikan gambar di bawah ini. Besar sudut pusat AOB adalah 90°, kemudian jari-jarinya = 21 cm. Hitunglah luas daerah yang diarsir.
5. Diketahui ∠OAB = 55° dan AB = BC. Tentukanlah besar:
a. ∠AOB
b. ∠ACB
c. ∠ABC
6. Perhatikan gambar di samping Diketahui ∠AEB = 62°. Hitunglah besar: ∠ADB, ∠ACB, dan ∠ABC
7. Suatu pabrik membuat biskuit yang berbentuk lingkaran padat dengan diameter 5 cm. Sebagai variasi, pabrik tersebut juga ingin membuat biskuit dengan ketebalan sama namun berbentuk juring lingkaran dengan sudut pusat 90°. Tentukan diameter biskuit tersebut agar bahan produksinya sama dengan biskuit yang berbentuk lingkaran.
8. Pak Santoso memiliki lahan di belakang rumahnya berbentuk persegi dengan ukuran panjang sisi 28 × 28 m2 . Taman tersebut sebagian akan dibuat kolam (tidak diarsir) dan sebagian lagi rumput hias (diarsir).
9. Diketahui bahwa luas daerah yang diarsir setengah dari luas daerah yang tidak diarsir. Tentukan panjang AB dibagi panjang AC.
10. Diketahui persegi ABCD tersusun dari empat 4 persegi kecil sama ukuran dengan panjang sisi = 10 cm. Tentukan luas daerah yang diarsir berikut. Jelaskan jawabanmu
Kunci Jawaban Matematika Kelas 8 Halaman 113 - 120 Uji Kompetensi 7
Kunci Jawaban Pilihan Ganda Uji Kompetensi 7 Matematika Kelas 8 Halaman 113
1. B. 10 cm
2. C. 21
3. B. 90°
4. B. 10,5 cm
5. A. 11 cm
6. B. 125°
7. D. 24°
8. D. Sekitar 5.000.000 putaran
9. B. 148 cm
10. C. 273 cm2
11. A. 12,5
12. C. 6
13. C. 1,6
14. A. 41
15. D. 10 cm dan 2 cm
16. C. 24 cm dan 4 cm
17. A. 1 cm
18. D. 220 cm
19. C. 2 cm dan 3 cm
20. A. 2 cm
Kunci Jawaban Esai Uji Kompetensi 7 Matematika Kelas 8 Halaman 118
1. Perhatikan gambar di samping. Diketahui lingkaran dengan pusat G dan berjari-jari 26 cm. Talibusur AC dan DF berjarak sama-sama 10 cm terhadap G. Tentukan panjang:
a. AC
b. DE
Jawaban :
a)
Perhatikan gambar tersebut, dengan menggunakan rumus Pythagoras kita dapat menemukan berapa panjang AC dengan sisi miringnya adalah AF, dan sisi alasnya adalah CF.
AC = √(AF2 - CF2)
= √((26 + 26)2 - (10 + 10)2)
= √(522 - 202)
= √(2704 - 400)
= √2304
= 48 cm
Jadi, panjang AB adalah 48 cm.
b)
DE = AC / 2
= 48 / 2
= 24 cm
Jadi, panjang DE adalah 24 cm.
a)
Perhatikan gambar tersebut, dengan menggunakan rumus Pythagoras kita dapat menemukan berapa panjang AC dengan sisi miringnya adalah AF, dan sisi alasnya adalah CF.
AC = √(AF2 - CF2)
= √((26 + 26)2 - (10 + 10)2)
= √(2704 - 400)
= √2304
= 48 cm
Jadi, panjang AB adalah 48 cm.
b)
DE = AC / 2
= 48 / 2
= 24 cm
Jadi, panjang DE adalah 24 cm.
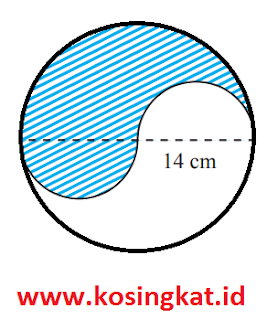
2. Tentukan keliling daerah yang diarsir pada bangun berikut.
Jawaban :
Dari gambar tersebut dapat kita ketahui keliling daerah yang diarsir = panjang setengah keliling lingkaran besar + panjang keliling lingkaran kecil
Keliling diarsir = (1/2 x 2 x π x r) + (2 x π x r)
= (1/2 x 2 x 22/7 x 14) + (2 x 22/7 x 7)
= 44 + 44
= 88 cm
Jadi, panjang keliling daerah yang diarsir tersebut adalah 88 cm.
Dari gambar tersebut dapat kita ketahui keliling daerah yang diarsir = panjang setengah keliling lingkaran besar + panjang keliling lingkaran kecil
Keliling diarsir = (1/2 x 2 x π x r) + (2 x π x r)
= (1/2 x 2 x 22/7 x 14) + (2 x 22/7 x 7)
= 44 + 44
= 88 cm
Jadi, panjang keliling daerah yang diarsir tersebut adalah 88 cm.
3. Amati gambar di bawah ini. Tentukan keliling dan luas daerah yang diarsir.
Jawaban :
Keliling diarsir = keliling 1 lingkaran penuh + 1/2 keliling persegi
= (2 x π x r) + (1/2 x 4 x s)
= (2 x 3,14 x 5) + (1/2 x 4 x 10)
= 31,4 + 20
= 51,4 cm
Luas diarsir = luas 1 persegi penuh + 1/2 luas lingkaran
= (s x s) + (1/2 x π x r x r)
= (10 x 10) + (1/2 x 3,14 x 5 x 5)
= 100 + 39,25
= 139,25 cm2
Jadi, keliling dan luas daerah yang diarsir adalah 51,4 cm dan 139,25 cm2.
Keliling diarsir = keliling 1 lingkaran penuh + 1/2 keliling persegi
= (2 x π x r) + (1/2 x 4 x s)
= (2 x 3,14 x 5) + (1/2 x 4 x 10)
= 31,4 + 20
= 51,4 cm
Luas diarsir = luas 1 persegi penuh + 1/2 luas lingkaran
= (s x s) + (1/2 x π x r x r)
= (10 x 10) + (1/2 x 3,14 x 5 x 5)
= 100 + 39,25
= 139,25 cm2
Jadi, keliling dan luas daerah yang diarsir adalah 51,4 cm dan 139,25 cm2.
4. Perhatikan gambar di bawah ini. Besar sudut pusat AOB adalah 90°, kemudian jari-jarinya = 21 cm. Hitunglah luas daerah yang diarsir.
Jawaban :
Luas diarsir = 1/4 luas lingkaran - luas segitiga
= (1/4 x π x r x r) - (1/2 x panjang alas x tinggi)
= (1/4 x 22/7 x 21 x 21) - (1/2 x 21 x 21)
= 346,5 - 220,5
= 126 cm2
Luas diarsir = 1/4 luas lingkaran - luas segitiga
= (1/4 x π x r x r) - (1/2 x panjang alas x tinggi)
= (1/4 x 22/7 x 21 x 21) - (1/2 x 21 x 21)
= 346,5 - 220,5
= 126 cm2
Jadi, luas daerah yang diarsir adalah 126 cm2.
5. Diketahui ∠OAB = 55° dan AB = BC. Tentukanlah besar:
a. ∠AOB
b. ∠ACB
c. ∠ABC
Jawaban :
a)
∠AOB = 180° - (2 × ∠OAB)
= 180° - (2 × 55°)
= 180° - 110°
= 70°
Jadi, besar sudut AOB adalah 70°.
b)
∠ACB = 1/2 × ∠AOB
= 1/2 × 70°
= 35°
Jadi, besar sudut ACB adalah 35°.
c)
∠ABC = 180° - (2 × ∠ACB)
= 180° - (2 × 35°)
= 180° - 70°
= 110°
Jadi, besar sudut ABC adalah 110°.
a)
∠AOB = 180° - (2 × ∠OAB)
= 180° - (2 × 55°)
= 180° - 110°
= 70°
Jadi, besar sudut AOB adalah 70°.
b)
∠ACB = 1/2 × ∠AOB
= 1/2 × 70°
= 35°
Jadi, besar sudut ACB adalah 35°.
c)
∠ABC = 180° - (2 × ∠ACB)
= 180° - (2 × 35°)
= 180° - 70°
= 110°
Jadi, besar sudut ABC adalah 110°.
6. Perhatikan gambar di samping Diketahui ∠AEB = 62°. Hitunglah besar: ∠ADB, ∠ACB, dan ∠ABC
Jawaban :
Perhatikan titik E,D, dan C dari gambar tersebut dapat dilihat bahwa ketiga titik tersebut memiliki garis AB yang sama. Sehingga besar sudut AEB, ADB, dan ACB dapat dipastikan sama.
∠AEB = ∠ADB = ∠ACB = 62°
Perhatikan garis AC, garis AC merupakan diameter lingkaran, sudut yang menghadap diameter lingkaran besarnya adalah 90°.
∠ABC = 90°
Jadi, besar ∠ADB = 62°, ∠ACB = 62°, dan ∠ABC = 90°.
Perhatikan titik E,D, dan C dari gambar tersebut dapat dilihat bahwa ketiga titik tersebut memiliki garis AB yang sama. Sehingga besar sudut AEB, ADB, dan ACB dapat dipastikan sama.
∠AEB = ∠ADB = ∠ACB = 62°
Perhatikan garis AC, garis AC merupakan diameter lingkaran, sudut yang menghadap diameter lingkaran besarnya adalah 90°.
∠ABC = 90°
Jadi, besar ∠ADB = 62°, ∠ACB = 62°, dan ∠ABC = 90°.
Jawaban :
Luas biskuit lingkaran = π x r x r
= 3,14 x 2,5 x 2,5
= 19,625 cm2
Luas juring lingkaran = luas biskuit lingkaran
90°/360 ° x π x r x r = 19,625
1/4 x 3,14 x r2 = 19,625
r2 = 19,625 x 4 / 3,14
r = √25
r = 5 cm
Diameter biskuit = 2 x r
= 2 x 5
= 10 cm
Jadi, diameter biskuit tersebut adalah 10 cm.
Luas biskuit lingkaran = π x r x r
= 3,14 x 2,5 x 2,5
= 19,625 cm2
Luas juring lingkaran = luas biskuit lingkaran
90°/360 ° x π x r x r = 19,625
1/4 x 3,14 x r2 = 19,625
r2 = 19,625 x 4 / 3,14
r = √25
r = 5 cm
Diameter biskuit = 2 x r
= 2 x 5
= 10 cm
Jadi, diameter biskuit tersebut adalah 10 cm.
8. Pak Santoso memiliki lahan di belakang rumahnya berbentuk persegi dengan ukuran panjang sisi 28 × 28 m2 . Taman tersebut sebagian akan dibuat kolam (tidak diarsir) dan sebagian lagi rumput hias (diarsir).
Jawaban :
a)
Keliling lahan = keliling 1 lingkaran penuh + 1/2 x 2 panjang sisi persegi
= (2 x π x r) + (1/2 x 2 x s)
= (2 x 22/7 x 14 + (1/2 x 2 x 28)
= 88 + 28
= 116 m
Jadi, keliling lahan rumput Pak Santoso adalah 116 m.
b)
Perhatikan gambar diatas dari gambar tersebut, luas lahan = luas persegi - luas lingkaran
Luas lahan = (s x s) - (π x r x r)
= (28 x 28) - (22/7 x 14 x 14)
= 784 - 616
= 168 m2
Anggaran = (biaya pemasangan x luas lahan) + biaya tukang
= (50.000 x 168) + 250.000
= 8.400.000 + 250.000
= 8.650.000
Jadi, anggaran yang harus disiapkan Pak Santoso adalah Rp.8.650.000,00.
a)
Keliling lahan = keliling 1 lingkaran penuh + 1/2 x 2 panjang sisi persegi
= (2 x π x r) + (1/2 x 2 x s)
= (2 x 22/7 x 14 + (1/2 x 2 x 28)
= 88 + 28
= 116 m
Jadi, keliling lahan rumput Pak Santoso adalah 116 m.
b)
Perhatikan gambar diatas dari gambar tersebut, luas lahan = luas persegi - luas lingkaran
Luas lahan = (s x s) - (π x r x r)
= (28 x 28) - (22/7 x 14 x 14)
= 784 - 616
= 168 m2
Anggaran = (biaya pemasangan x luas lahan) + biaya tukang
= (50.000 x 168) + 250.000
= 8.400.000 + 250.000
= 8.650.000
Jadi, anggaran yang harus disiapkan Pak Santoso adalah Rp.8.650.000,00.
9. Diketahui bahwa luas daerah yang diarsir setengah dari luas daerah yang tidak diarsir. Tentukan panjang AB dibagi panjang AC.
10. Diketahui persegi ABCD tersusun dari empat 4 persegi kecil sama ukuran dengan panjang sisi = 10 cm. Tentukan luas daerah yang diarsir berikut. Jelaskan jawabanmu
Jawaban :
Dari gambar tersebut, jika kita perhatikan baik-baik dengan menggabungkan masing-masing potongan daerah yang diarsir akan membentuk persegi kecil yang ukurannya 1/4 persegi besar.
Luas daerah yang diarsir = 1/4 x luas persegi
= 1/4 x (s x s)
= 1/4 x (20 x 20)
= 1/4 x 400
= 100 cm2
Jadi, luas daerah yang diarsir adalah 100 cm2
Dari gambar tersebut, jika kita perhatikan baik-baik dengan menggabungkan masing-masing potongan daerah yang diarsir akan membentuk persegi kecil yang ukurannya 1/4 persegi besar.
Luas daerah yang diarsir = 1/4 x luas persegi
= 1/4 x (s x s)
= 1/4 x (20 x 20)
= 1/4 x 400
= 100 cm2
Jadi, luas daerah yang diarsir adalah 100 cm2




Belum ada Komentar untuk "Kunci Jawaban Matematika Kelas 8 Halaman 113 - 120 Uji Kompetensi 7"
Posting Komentar