Kunci Jawaban Matematika Kelas 8 Halaman 77 - 78 Ayo Kita Berlatih 7.2
Berikut ini adalah pembahasan dan Kunci Jawaban Matematika Kelas 8 Semester 2 Halaman 77 - 78. Bab 7 Lingkaran Ayo Kita berlatih 7.2 Hal 77 - 78 Nomor 1 - 2 PG dan 1 - 7 Esai. Kunci jawaban ini dibuat untuk membantu mengerjakan soal matematika bagi kelas 8 di semester 2 halaman 77 - 78. Semoga dengan adanya pembahasan serta kunci jawaban ini adik-adik kelas 8 dapat menyelesaikan tugas Lingkaran Kelas 8 Halaman 77 - 78 yang diberikan oleh bapak ibu/guru. Kunci Jawaban MTK Kelas 8 Semester 2.
2. Diketahui segitiga ABC, dengan titik-titik sudutnya berada pada lingkaran O. Jika sisi AB melalui pusat lingkaran O, maka besar sudut BCA adalah ...
Essai
1. Suatu sudut keliling dan sudut pusat menghadap busur yang sama. Jika sudut pusat berukuran 130°, maka besar sudut keliling tersebut adalah .
2. Diketahui sudut pusat POQ dan sudut keliling PAQ sama-sama menghadap busur PQ. Besar sudut PAQ adalah 80° . Tentukan besar sudut POQ.
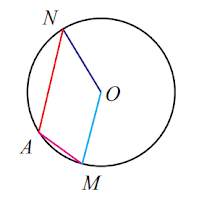
3. Perhatikan gambar di samping. Diketahui m∠MAN adalah 120° . Tentukan besar m∠MON.
4. Perhatikan segiempat PQRS di samping. Diketahui m∠PQR = 125°, m∠QRS = 78°. Tentukan:
a. m∠SPQ
b. m∠RSP
5. Perhatikan lingkaran O di samping. Diketahui m∠BAD = x + 20, m∠BCD = 3x Tentukan:
a. m∠BOD minor
b. m∠BOD mayor
6. Suatu lingkaran dibagi menjadi tiga sudut pusat dengan perbandingan 3 : 5 : 10. Tentukan ukuran masing-masing sudut pusat tersebut.
7. Sudut pusat 1, 2, dan 3 mempunyai perbandingan 2 : 3 : 4. Tentukan ukuran masing-masing sudut pusat tersebut.
Kunci Jawaban Matematika Kelas 8 Halaman 77 - 78 Ayo Kita Berlatih 7.2
Pilihan Ganda
1. Diketahui pada lingkaran O, terdapat sudut pusat AOB dan sudut keliling ACB. Jika besar sudut AOB adalah 30° , maka besar sudut ACB adalah ...
Jawaban :
Sudut pusat = 2 x sudut keliling
AOB = 2 x ACB
30° = 2 x ACB
ACB = 30° / 2
ACB = 15°
Jadi, jawabannya adalah A.15°.
Sudut pusat = 2 x sudut keliling
AOB = 2 x ACB
30° = 2 x ACB
ACB = 30° / 2
ACB = 15°
Jadi, jawabannya adalah A.15°.
2. Diketahui segitiga ABC, dengan titik-titik sudutnya berada pada lingkaran O. Jika sisi AB melalui pusat lingkaran O, maka besar sudut BCA adalah ...
Jawaban :
BOA = 2 × BCA
180° = 2 × BCA
BCA= 180° / 2
BCA = 90°
Jadi, jawabannya adalah C.90°
BOA = 2 × BCA
180° = 2 × BCA
BCA= 180° / 2
BCA = 90°
Jadi, jawabannya adalah C.90°
Essai
1. Suatu sudut keliling dan sudut pusat menghadap busur yang sama. Jika sudut pusat berukuran 130°, maka besar sudut keliling tersebut adalah .
Jawaban :
Sudut pusat = 2 x sudut keliling
130° = 2 x sudut keliling
sudut keliling = 130° / 2
sudut keliling = 65°
Jadi, besar sudut kelilingnya adalah 65°.
Sudut pusat = 2 x sudut keliling
130° = 2 x sudut keliling
sudut keliling = 130° / 2
sudut keliling = 65°
Jadi, besar sudut kelilingnya adalah 65°.
2. Diketahui sudut pusat POQ dan sudut keliling PAQ sama-sama menghadap busur PQ. Besar sudut PAQ adalah 80° . Tentukan besar sudut POQ.
Jawaban :
Sudut pusat = 2 x sudut keliling
POQ = 2 x PAQ
POQ = 2 x 80°
POQ = 160°
Jadi, besar sudut PAQ adalah 160°.
Sudut pusat = 2 x sudut keliling
POQ = 2 x PAQ
POQ = 2 x 80°
POQ = 160°
Jadi, besar sudut PAQ adalah 160°.
3. Perhatikan gambar di samping. Diketahui m∠MAN adalah 120° . Tentukan besar m∠MON.
Jawaban :
m∠MON = 360° - sudut keliling MON
= 360° - (2 x 120°)
= 360° - 240°
= 120°
Jadi, besar m∠MON adalah 120°.
m∠MON = 360° - sudut keliling MON
= 360° - (2 x 120°)
= 360° - 240°
= 120°
Jadi, besar m∠MON adalah 120°.
4. Perhatikan segiempat PQRS di samping. Diketahui m∠PQR = 125°, m∠QRS = 78°. Tentukan:
a. m∠SPQ
b. m∠RSP
Jawaban :
a)
m∠QRS + m∠SPQ = 180°
78 + m∠SPQ = 180°
m∠SPQ = 180 - 78°
m∠SPQ = 102°
Jadi, besar sudut SPQ adalah 102°.
b)
m∠PQR + m∠RSP = 180°
125 + m∠RSP = 180°
m∠RSP = 180 - 125°
m∠RSP = 55°
Jadi, besar sudut RSP adalah 55°.
a)
m∠QRS + m∠SPQ = 180°
78 + m∠SPQ = 180°
m∠SPQ = 180 - 78°
m∠SPQ = 102°
Jadi, besar sudut SPQ adalah 102°.
b)
m∠PQR + m∠RSP = 180°
125 + m∠RSP = 180°
m∠RSP = 180 - 125°
m∠RSP = 55°
Jadi, besar sudut RSP adalah 55°.
5. Perhatikan lingkaran O di samping. Diketahui m∠BAD = x + 20, m∠BCD = 3x Tentukan:
a. m∠BOD minor
b. m∠BOD mayor
Jawaban :
a)
m∠BOD minor = 2x + 40
= (2 x 40) + 40
= 80 + 40
= 120°
Jadi, besar BOD minor adalah 120°.
b)
m∠BOD mayor = 6x
= 6 x 40
= 240°
Jadi, besar BOD mayor adalah 240°.
a)
m∠BOD minor = 2x + 40
= (2 x 40) + 40
= 80 + 40
= 120°
Jadi, besar BOD minor adalah 120°.
b)
m∠BOD mayor = 6x
= 6 x 40
= 240°
Jadi, besar BOD mayor adalah 240°.
6. Suatu lingkaran dibagi menjadi tiga sudut pusat dengan perbandingan 3 : 5 : 10. Tentukan ukuran masing-masing sudut pusat tersebut.
Jawaban :
Jumlah besar sudut lingkaran = 360°
Jumlah perbandingan = 3 + 5 + 10 = 18
Sudut 1 = 3 / 18 x 360°
= 60°
Sudut 2 = 5 / 18 x 360°
= 100°
Sudut 3 10 / 18 x 360°
= 200°
Jadi, masing-masing ukuran sudut pusat tersebut adalah 60° : 100° : 200°.
Jumlah besar sudut lingkaran = 360°
Jumlah perbandingan = 3 + 5 + 10 = 18
Sudut 1 = 3 / 18 x 360°
= 60°
Sudut 2 = 5 / 18 x 360°
= 100°
Sudut 3 10 / 18 x 360°
= 200°
Jadi, masing-masing ukuran sudut pusat tersebut adalah 60° : 100° : 200°.
7. Sudut pusat 1, 2, dan 3 mempunyai perbandingan 2 : 3 : 4. Tentukan ukuran masing-masing sudut pusat tersebut.
Jawaban :
Jumlah besar sudut lingkaran = 360°
Jumlah perbandingan = 2 + 3 + 4 = 9
Sudut 1 = 2 / 9 x 360°
= 80°
Sudut 2 = 3 / 9 x 360°
= 120°
Sudut 3 4 / 9 x 360°
= 160°
Jadi, masing-masing ukuran sudut pusat tersebut adalah 80° : 120° : 160°.
Jumlah besar sudut lingkaran = 360°
Jumlah perbandingan = 2 + 3 + 4 = 9
Sudut 1 = 2 / 9 x 360°
= 80°
Sudut 2 = 3 / 9 x 360°
= 120°
Sudut 3 4 / 9 x 360°
= 160°
Jadi, masing-masing ukuran sudut pusat tersebut adalah 80° : 120° : 160°.


Belum ada Komentar untuk "Kunci Jawaban Matematika Kelas 8 Halaman 77 - 78 Ayo Kita Berlatih 7.2"
Posting Komentar