Kunci Jawaban Matematika Kelas 8 Halaman 165, 166 Ayo Kita Berlatih 8.4
Berikut ini adalah pembahasan dan Kunci Jawaban Matematika Kelas 8 Semester 2 Halaman 165, 166. Bab 8 Bangun Ruang Sisi Datar Ayo Kita berlatih 8.4 Hal 165, 166 Nomor 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Kunci jawaban ini dibuat untuk membantu mengerjakan soal matematika bagi kelas 8 di semester 2 halaman 165, 166. Semoga dengan adanya pembahasan serta kunci jawaban ini adik-adik kelas 8 dapat menyelesaikan tugas Bangun Ruang Sisi Datar Kelas 8 Halaman 165, 166 yang diberikan oleh bapak ibu/guru. Kunci Jawaban MTK Kelas 8 Semester 2.
2. Gambar di samping menunjukkan tumpukan batu dengan ukuran sama. Pada tumpukan batu tersebut terdapat lubang. Berapa banyak tumpukan batu untuk menutupi lubang tersebut?
3. Tentukan volume kubus yang luas alasnya 49 cm2 .
4. Tentukan volume balok yang berukuran 13 cm × 15 cm × 17 cm
5. Sebuah bak mandi berbentuk kubus memiliki panjang rusuk 1,4 m. Tentukan banyak air yang dibutuhkan untuk mengisi bak mandi tersebut hingga penuh.
6. Sebuah kolam berbentuk balok berukuran panjang 5 m, lebar 3 m, dan dalam 2 m. Banyak air maksimal yang dapat ditampung adalah ….
A. 62 m3
B. 40 m3
C. 30 m3
D. 15 m3
7. Sebuah akuarium berbentuk balok memiliki ukuran panjang 74 cm dan tinggi 42 cm. Jika volume air di dalam akuarium tersebut adalah 31.080 cm3 , tentukan lebar akuarium tersebut.
8. Diketahui volume sebuah balok 72 cm3 . Tentukan luas permukaan minimal yang dapat dimiliki oleh balok tersebut.
9. Jika keliling alas sebuah akuarium yang berbentuk kubus adalah 36 cm, maka tentukan volume akuarium tersebut.
10. Perbandingan panjang, lebar, dan tinggi sebuah balok adalah 5 : 3 : 4. Jika volume balok 480 cm3 , maka tentukan luas permukaan balok terebut.
Terima kasih telah mengunjungi KoSingkat untuk mengakes kunci jawaban matematika kelas 8 halaman 165, 166 semester 2 ayo kita berlatih 8.4. Semoga kunci jawaban dan pembahasan yang diberikan berguna bagi adik-adik dalam mengerjakan tugas yang diberikan.
Kunci Jawaban Matematika Kelas 8 Halaman 165, 166 Ayo Kita Berlatih 8.4
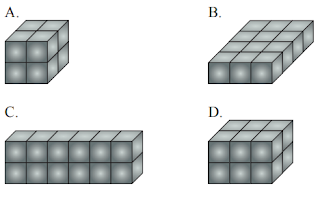
1. Semua balok kecil memiliki ukuran yang sama. Tumpukan blok yang manakah yang memiliki volume yang berbeda dari yang lain?
Jawaban :
Balok A : panjang = 2, lebar = 2, tinggi = 2
Volume Balok A = p x l x t
= 2 x 2 x 2
= 8
Balok B : panjang = 4, lebar = 3, tinggi = 1
Volume Balok A = p x l x t
= 4 x 3 x 1
= 12
Balok C : panjang = 6, lebar = 1, tinggi = 2
Volume Balok A = p x l x t
= 6 x 1 x 2
= 12
Balok D : panjang = 3, lebar = 2, tinggi = 2
Volume Balok A = p x l x t
= 3 x 2 x 2
= 12
Jadi, tumpukan balok yang memiliki volume berbeda dari yang lain adalah Balok A.
Balok A : panjang = 2, lebar = 2, tinggi = 2
Volume Balok A = p x l x t
= 2 x 2 x 2
= 8
Balok B : panjang = 4, lebar = 3, tinggi = 1
Volume Balok A = p x l x t
= 4 x 3 x 1
= 12
Balok C : panjang = 6, lebar = 1, tinggi = 2
Volume Balok A = p x l x t
= 6 x 1 x 2
= 12
Balok D : panjang = 3, lebar = 2, tinggi = 2
Volume Balok A = p x l x t
= 3 x 2 x 2
= 12
Jadi, tumpukan balok yang memiliki volume berbeda dari yang lain adalah Balok A.
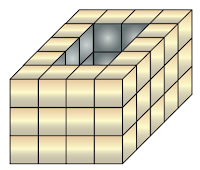
2. Gambar di samping menunjukkan tumpukan batu dengan ukuran sama. Pada tumpukan batu tersebut terdapat lubang. Berapa banyak tumpukan batu untuk menutupi lubang tersebut?
A. 6
B. 12
C. 15
D. 18
Jawaban :
Panjang lubang = 5 - 2
= 3
Lebar lubang = 4 - 2
= 2
Tinggi lubang = 3
Banyak batu untuk menutup lubang = p x l x t
= 3 x 2 x 3
= 18
Jadi, banyak tumpukan batu yang dibutuhkan untuk menutupi lubang tersebut adalah D.18.
Panjang lubang = 5 - 2
= 3
Lebar lubang = 4 - 2
= 2
Tinggi lubang = 3
Banyak batu untuk menutup lubang = p x l x t
= 3 x 2 x 3
= 18
Jadi, banyak tumpukan batu yang dibutuhkan untuk menutupi lubang tersebut adalah D.18.
3. Tentukan volume kubus yang luas alasnya 49 cm2 .
Jawaban :
Panjang, lebar, dan tinggi sebuah kubus adalah sama.
Sehingga,
Luas alas = s x s
49 = s2
s = √49
s = 7
Volume kubus = s x s x s
= 7 x 7 x 7
= 343 cm3
Jadi, volume kubus yang luas alasnya 49 cm2 adalah 343 3.
Panjang, lebar, dan tinggi sebuah kubus adalah sama.
Sehingga,
Luas alas = s x s
49 = s2
s = √49
s = 7
Volume kubus = s x s x s
= 7 x 7 x 7
= 343 cm3
Jadi, volume kubus yang luas alasnya 49 cm2 adalah 343 3.
4. Tentukan volume balok yang berukuran 13 cm × 15 cm × 17 cm
Jawaban :
Volume balok = p x l x t
= 13 x 15 x 17
= 3315 cm3
Jadi, volume balok yang berukuran 13 cm × 15 cm × 17 cm adalah 3315 cm3.
Volume balok = p x l x t
= 13 x 15 x 17
= 3315 cm3
Jadi, volume balok yang berukuran 13 cm × 15 cm × 17 cm adalah 3315 cm3.
5. Sebuah bak mandi berbentuk kubus memiliki panjang rusuk 1,4 m. Tentukan banyak air yang dibutuhkan untuk mengisi bak mandi tersebut hingga penuh.
Jawaban :
Volume bak mandi = s x s x s
= 1,4 x 1,4 x 1,4
= 2,744 m3
1 m3 = 1000 liter
2,744 m3 = 2,744 x 1000
= 2744 liter
Jadi, banyak air yang dibutuhkan untuk mengisi bak mandi tersebut hingga penuh adalah 2744 liter.
Volume bak mandi = s x s x s
= 1,4 x 1,4 x 1,4
= 2,744 m3
1 m3 = 1000 liter
2,744 m3 = 2,744 x 1000
= 2744 liter
Jadi, banyak air yang dibutuhkan untuk mengisi bak mandi tersebut hingga penuh adalah 2744 liter.
6. Sebuah kolam berbentuk balok berukuran panjang 5 m, lebar 3 m, dan dalam 2 m. Banyak air maksimal yang dapat ditampung adalah ….
A. 62 m3
B. 40 m3
C. 30 m3
D. 15 m3
Jawaban :
Volume kolam balok = p x l x t
= 5 x 3 x 2
= 30 m3
Jadi, banyak air maksimal yang dapat ditampung adalah C. 30 m3.
Volume kolam balok = p x l x t
= 5 x 3 x 2
= 30 m3
Jadi, banyak air maksimal yang dapat ditampung adalah C. 30 m3.
7. Sebuah akuarium berbentuk balok memiliki ukuran panjang 74 cm dan tinggi 42 cm. Jika volume air di dalam akuarium tersebut adalah 31.080 cm3 , tentukan lebar akuarium tersebut.
Jawaban :
Volume akuarium balok = p x l x t
31.080 = 74 x l x 42
l = 31.080/(74 x 42)
= 10 cm
Jadi, lebar akuarium tersebut adalah 10 cm.
Volume akuarium balok = p x l x t
31.080 = 74 x l x 42
l = 31.080/(74 x 42)
= 10 cm
Jadi, lebar akuarium tersebut adalah 10 cm.
8. Diketahui volume sebuah balok 72 cm3 . Tentukan luas permukaan minimal yang dapat dimiliki oleh balok tersebut.
Jawaban :
Volume balok = p x l x t
Luas permukaan balok = 2 x (pl + pt + lt)
Untuk mencari permukaan minimal maka p, l, t harus memiliki selisih seminimal mungkin. Oleh karena itu pertama kita dapat menentukan terlebih dahulu p, l, t dengan mencari 3 faktor dari 72.
Kemungkinan yang paling tepat adalah p=3, l=4, dan t=6.
Luas permukaan balok = 2 x ((3x4) + (3x6) + (4x6))
= 2 x (12 + 18 + 24)
= 2 x 54
= 108 cm2
Jadi, luas permukaan minimal yang dapat dimiliki oleh balok tersebut adalah 108 cm2.
Volume balok = p x l x t
Luas permukaan balok = 2 x (pl + pt + lt)
Untuk mencari permukaan minimal maka p, l, t harus memiliki selisih seminimal mungkin. Oleh karena itu pertama kita dapat menentukan terlebih dahulu p, l, t dengan mencari 3 faktor dari 72.
Kemungkinan yang paling tepat adalah p=3, l=4, dan t=6.
Luas permukaan balok = 2 x ((3x4) + (3x6) + (4x6))
= 2 x (12 + 18 + 24)
= 2 x 54
= 108 cm2
Jadi, luas permukaan minimal yang dapat dimiliki oleh balok tersebut adalah 108 cm2.
9. Jika keliling alas sebuah akuarium yang berbentuk kubus adalah 36 cm, maka tentukan volume akuarium tersebut.
Jawaban :
Keliling alas kubus = 4 x s
36 = 4 x s
s = 36/4
s = 9 cm
Volume kubus = s x s x s
= 9 x 9 x 9
= 729 cm3
1cm3 = 0,001 liter
729 cm3 = 729 x 0,001
= 0,729 liter
Jadi, volume akuarium tersebut adalah 0,729 liter.
Keliling alas kubus = 4 x s
36 = 4 x s
s = 36/4
s = 9 cm
Volume kubus = s x s x s
= 9 x 9 x 9
= 729 cm3
1cm3 = 0,001 liter
729 cm3 = 729 x 0,001
= 0,729 liter
Jadi, volume akuarium tersebut adalah 0,729 liter.
10. Perbandingan panjang, lebar, dan tinggi sebuah balok adalah 5 : 3 : 4. Jika volume balok 480 cm3 , maka tentukan luas permukaan balok terebut.
Jawaban :
Misalkan,
panjang balok = 5x
lebar balok = 3x
tinggi balok = 4x
Volume balok = p x l x t
480 = 5x x 3x x 4x
480 = 60 x3
x3 = 480/60
x3 = 8
x = akar pangkat 3 dari 8
x = 2
panjang balok = 5x = 5 x 2 = 10
lebar balok = 3x = 3 x 2 = 6
tinggi balok = 4x = 4 x 2 = 8
Luas permukaan balok = 2 x (pl + pt + lt )
= 2 x ((10 x 6) + (10 x 8) + (6 x 8))
= 2 x (60 + 80 + 48 )
= 2 x 188
= 376 cm3
Jadi, luas permukaan balok tersebut adalah 376 cm3.
Misalkan,
panjang balok = 5x
lebar balok = 3x
tinggi balok = 4x
Volume balok = p x l x t
480 = 5x x 3x x 4x
480 = 60 x3
x3 = 480/60
x3 = 8
x = akar pangkat 3 dari 8
x = 2
panjang balok = 5x = 5 x 2 = 10
lebar balok = 3x = 3 x 2 = 6
tinggi balok = 4x = 4 x 2 = 8
Luas permukaan balok = 2 x (pl + pt + lt )
= 2 x ((10 x 6) + (10 x 8) + (6 x 8))
= 2 x (60 + 80 + 48 )
= 2 x 188
= 376 cm3
Jadi, luas permukaan balok tersebut adalah 376 cm3.
Terima kasih telah mengunjungi KoSingkat untuk mengakes kunci jawaban matematika kelas 8 halaman 165, 166 semester 2 ayo kita berlatih 8.4. Semoga kunci jawaban dan pembahasan yang diberikan berguna bagi adik-adik dalam mengerjakan tugas yang diberikan.
Belum ada Komentar untuk "Kunci Jawaban Matematika Kelas 8 Halaman 165, 166 Ayo Kita Berlatih 8.4"
Posting Komentar