Kunci Jawaban Matematika Kelas 8 Halaman 153, 154 Ayo Kita Berlatih 8.3
Berikut ini adalah pembahasan dan Kunci Jawaban Matematika Kelas 8 Semester 2 Halaman 153, 154. Bab 8 Bangun Ruang Sisi Datar Ayo Kita berlatih 8.3 Hal 153, 154 Nomor 7, 8, 9, 10, 11, 12. Kunci jawaban ini dibuat untuk membantu mengerjakan soal matematika bagi kelas 8 di semester 2 halaman 153, 154. Semoga dengan adanya pembahasan serta kunci jawaban ini adik-adik kelas 8 dapat menyelesaikan tugas Bangun Ruang Sisi Datar Kelas 8 Halaman 153, 154 yang diberikan oleh bapak ibu/guru. Kunci Jawaban MTK Kelas 8 Semester 2.
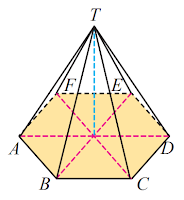
8. Perhatikan gambar limas segienam T.ABCEF berikut. Diketahui pada gambar limas tersebut merupakan limas segienam beraturan dengan panjang AB = 10 cm dan TO = 30 cm. Tentukan luas permukaan limas tersebut.
9. Alas sebuah limas segi empat beraturan berbentuk persegi. Jika tinggi segitiga 20 cm dan tinggi limas 16 cm, tentukan luas permukaan limas.
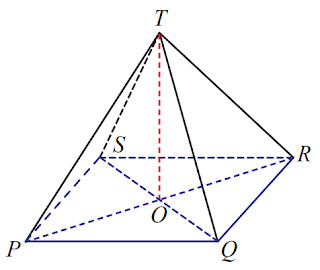
10. Perhatikan limas segiempat T.PQRS berikut.
Segiempat PQRS pada limas tersebut merupakan suatu persegi. Diketahui luas permukaannya adalah 360 cm2 . Jika tinggi limas tersebut merupakan bilangan bulat, maka tentukan kemungkinan panjang sisi alas dan tinggi limas tersebut.
11. Suatu limas segiempat beraturan sisi tegaknya terdiri atas empat segitiga sama kaki yang sama besar dan sama bentuknya. Diketahui luas salah satu segitiga itu 135 cm2 dan tinggi segitiga dari puncak limas 12 cm. Hitunglah luas permukaan limas.
12. Gambar di bawah menunjukkan sebuah kubus dengan panjang rusuk 5 cm yang dipotong sehingga salah satu bagiannya berbentuk limas segitiga (tetrahedron). Tentukan luas permukaan kedua bangun hasil perpotongannya.
Kunci Jawaban Matematika Kelas 8 Halaman 153, 154 Ayo Kita Berlatih 8.3
7. Diketahui luas permukaan limas dengan alas berbentuk persegi adalah 96 cm2 . Jika tinggi limas tersebut 4 cm, maka tentukan kemungkinan luas seluruh bidang tegak limas tersebut.
Jawaban :
Tinggi segitiga = m
m = √(t2 + (s/2)2)
= √(42 + (s/2)2)
= √(16 + s2/4)
Luas permukaan limas = luas alas + luas bidang tegak
96 = ( s x s ) + luas bidang tegak
96 = (6 x 6 ) + luas bidang tegak
luas bidang tegak = 96 - 36
= 60 cm2
Jadi, luas seluruh bidang tegak limas tersebut adalah 60 cm2.
Tinggi segitiga = m
m = √(t2 + (s/2)2)
= √(42 + (s/2)2)
= √(16 + s2/4)
Luas permukaan limas = luas alas + luas bidang tegak
96 = ( s x s ) + luas bidang tegak
96 = (6 x 6 ) + luas bidang tegak
luas bidang tegak = 96 - 36
= 60 cm2
Jadi, luas seluruh bidang tegak limas tersebut adalah 60 cm2.
8. Perhatikan gambar limas segienam T.ABCEF berikut. Diketahui pada gambar limas tersebut merupakan limas segienam beraturan dengan panjang AB = 10 cm dan TO = 30 cm. Tentukan luas permukaan limas tersebut.
Jawaban :
OP = √(OC2 - (CD/2)2)
= √(102 - (10/2)2)
= √(100 - 25)
= √75
= 5√3cm
TP = √(TO2 + OP2)
= √(302 + (5√3)2)
= √(900 + 75)
= √975
= 5√39cm
Luas permukaan = luas alas + (6 x luas segitiga )
= (3√3 x s2 / 2 ) + ( 6 x 1/2 x s x TP)
= (3√3 x 102 / 2 ) + ( 6 x 1/2 x 10 x 5√39)
= 150√3 + 150√39
= 150 (√3 + √39)
= 1196,55 cm2
Jadi, luas permukaan limas segienam tersebut adalah 1196,55 cm2.
Segitiga pada limas segienam adalah segitiga sama sisi, oleh karena itu :
= √(102 - (10/2)2)
= √(100 - 25)
= √75
= 5√3cm
TP = √(TO2 + OP2)
= √(302 + (5√3)2)
= √(900 + 75)
= √975
= 5√39cm
Luas permukaan = luas alas + (6 x luas segitiga )
= (3√3 x s2 / 2 ) + ( 6 x 1/2 x s x TP)
= (3√3 x 102 / 2 ) + ( 6 x 1/2 x 10 x 5√39)
= 150√3 + 150√39
= 150 (√3 + √39)
= 1196,55 cm2
Jadi, luas permukaan limas segienam tersebut adalah 1196,55 cm2.
9. Alas sebuah limas segi empat beraturan berbentuk persegi. Jika tinggi segitiga 20 cm dan tinggi limas 16 cm, tentukan luas permukaan limas.
Jawaban :
= 2 x √144
= 2 x 12
= 24cm
Luas permukaan = luas alas + ( 4 x luas segitiga )
= (24 x 24 ) + ( 4 x 1/2 x 24 x 20 )
= 576 + 960
= 1536 cm2
Jadi, luas permukaan limas segiempat tersebut adalah 1536 cm2.
Panjang sisi alas = 2 x √(KT2 - KO2)
= 2 x √(202 - 162)
= 2 x √(400 + 256)= 2 x √144
= 2 x 12
= 24cm
Luas permukaan = luas alas + ( 4 x luas segitiga )
= (24 x 24 ) + ( 4 x 1/2 x 24 x 20 )
= 576 + 960
= 1536 cm2
Jadi, luas permukaan limas segiempat tersebut adalah 1536 cm2.
10. Perhatikan limas segiempat T.PQRS berikut.
Segiempat PQRS pada limas tersebut merupakan suatu persegi. Diketahui luas permukaannya adalah 360 cm2 . Jika tinggi limas tersebut merupakan bilangan bulat, maka tentukan kemungkinan panjang sisi alas dan tinggi limas tersebut.
Jawaban :
Kemungkinan yang mungkin adalah,
panjang sisi alas = 10cm
tinggi limas = 12cm
tinggi bidang tegak = √(OT2 + (1/2 x sisi )2)
= √(122 + (1/2 x 10)2)
= √(144 + 25)
= √(169)
= 13cm
Luas permukaan = luas alas + (4 x luas segitiga )
= (10 x 10 ) + (4 x 1/2 x 10 x 13)
= 100 + 260
= 360cm2
Jadi, panjang sisi alas dan tinggi limas yang mungkin adalah panjang sisi alas = 10 cm dan tinggi limas = 12cm.
Kemungkinan yang mungkin adalah,
panjang sisi alas = 10cm
tinggi limas = 12cm
tinggi bidang tegak = √(OT2 + (1/2 x sisi )2)
= √(122 + (1/2 x 10)2)
= √(144 + 25)
= √(169)
= 13cm
Luas permukaan = luas alas + (4 x luas segitiga )
= (10 x 10 ) + (4 x 1/2 x 10 x 13)
= 100 + 260
= 360cm2
Jadi, panjang sisi alas dan tinggi limas yang mungkin adalah panjang sisi alas = 10 cm dan tinggi limas = 12cm.
11. Suatu limas segiempat beraturan sisi tegaknya terdiri atas empat segitiga sama kaki yang sama besar dan sama bentuknya. Diketahui luas salah satu segitiga itu 135 cm2 dan tinggi segitiga dari puncak limas 12 cm. Hitunglah luas permukaan limas.
Jawaban :
*tinggi segitiga pada soal salah, yang benar tingginya adalah 15cm*
s = panjang sisi alas
luas segitiga = 1/2 x 15 x s
135 = 7,5s
s = 135/7,5
= 18 cm
Luas permukaan = luas alas + (4 x luas segitiga)
= (18 x 18 ) + (4 x 135)
= 324 + 540
= 864 cm2
Jadi, luas permukaan limas tersebut adalah 864 cm2.
*tinggi segitiga pada soal salah, yang benar tingginya adalah 15cm*
s = panjang sisi alas
luas segitiga = 1/2 x 15 x s
135 = 7,5s
s = 135/7,5
= 18 cm
Luas permukaan = luas alas + (4 x luas segitiga)
= (18 x 18 ) + (4 x 135)
= 324 + 540
= 864 cm2
Jadi, luas permukaan limas tersebut adalah 864 cm2.
12. Gambar di bawah menunjukkan sebuah kubus dengan panjang rusuk 5 cm yang dipotong sehingga salah satu bagiannya berbentuk limas segitiga (tetrahedron). Tentukan luas permukaan kedua bangun hasil perpotongannya.
Jawaban :
*Perhatikan ilustrasi gambar diatas*
- warna merah adalah permukaan bangun 1 (persegi)
- warna biru adalah permukaan bangun 2 (segitiga)
- warna hijau adalah permukaan perpotongan kedua bangun
Panjang diagonal persegi = √(52 + 52)
= √(25 + 25)
= 5√2 cm
Tinggi segitiga hijau = √((1/2 x diagonal)2 + tinggi kubus2)
= √((1/2 x 5√2)2 + 52)
=√(5/2√2)2 + 52)
= √((25/4 x 2) + 25)
= √(12,5+ 25)
= √37,5
= 5√1,5 cm
Luas permukaan segitiga hijau = 1/2 x panjang diagonal x tinggi segitiga hijau
= 1/2 x 5√2 x 5√1,5
= 12,5√3
= 21,65 cm
Luas permukaan bangun 1 (persegi) = (4,5 x sisi x sisi) + luas segitiga hijau
= (4,5 x 5 x 5) + 21,65
= 112,5 + 21,65
= 134,15 cm2
Luas permukaan bangun 2 (segitiga) = (1,5 x sisi x sisi) + luas segitiga hijau
= (1,5 x 5 x 5) + 21,65
= 37,5 + 21,65
= 59,15 cm2
Luas permukaan kedua bangun = Luas permukaan 1 (persegi) + Luas permukaan 2 (segitiga)
= 134,15 + 59,15
= 193,3 cm2
Jadi, luas permukaan kedua bangun tersebut adalah 193,3 cm2.
*Perhatikan ilustrasi gambar diatas*
- warna merah adalah permukaan bangun 1 (persegi)
- warna biru adalah permukaan bangun 2 (segitiga)
- warna hijau adalah permukaan perpotongan kedua bangun
Panjang diagonal persegi = √(52 + 52)
= √(25 + 25)
= 5√2 cm
Tinggi segitiga hijau = √((1/2 x diagonal)2 + tinggi kubus2)
= √((1/2 x 5√2)2 + 52)
=√(5/2√2)2 + 52)
= √((25/4 x 2) + 25)
= √(12,5+ 25)
= √37,5
= 5√1,5 cm
Luas permukaan segitiga hijau = 1/2 x panjang diagonal x tinggi segitiga hijau
= 1/2 x 5√2 x 5√1,5
= 12,5√3
= 21,65 cm
Luas permukaan bangun 1 (persegi) = (4,5 x sisi x sisi) + luas segitiga hijau
= (4,5 x 5 x 5) + 21,65
= 112,5 + 21,65
= 134,15 cm2
Luas permukaan bangun 2 (segitiga) = (1,5 x sisi x sisi) + luas segitiga hijau
= (1,5 x 5 x 5) + 21,65
= 37,5 + 21,65
= 59,15 cm2
Luas permukaan kedua bangun = Luas permukaan 1 (persegi) + Luas permukaan 2 (segitiga)
= 134,15 + 59,15
= 193,3 cm2
Jadi, luas permukaan kedua bangun tersebut adalah 193,3 cm2.





2 Komentar untuk "Kunci Jawaban Matematika Kelas 8 Halaman 153, 154 Ayo Kita Berlatih 8.3"
yang sesuai donk jawaban ama soal
Halo soal nomor berapa yang salah ? akan kami perbaiki. Tetapi sebelum kami mempublish kunci jawaban kami selalu mengecek ulang jawaban dari para ahli. Dari masukan mereka, mereka menemukan bahwa memang terdapat soal dan kunci jawaban dari guru yang salah dan tidak sesuai, sehingga kami lebih memilih jawaban dari para ahli yang memang lebih benar. Terima Kasih
Posting Komentar