Kunci Jawaban Matematika Kelas 8 Halaman 134, 135 Ayo Kita Berlatih 8.1
Berikut ini adalah pembahasan dan Kunci Jawaban Matematika Kelas 8 Semester 2 Halaman 134, 135. Bab 8 Bangun Ruang Sisi Datar Ayo Kita berlatih 8.1 Hal 134, 135 Nomor 6, 7, 8, 9, 10. Kunci jawaban ini dibuat untuk membantu mengerjakan soal matematika bagi kelas 8 di semester 2 halaman 134, 135. Semoga dengan adanya pembahasan serta kunci jawaban ini adik-adik kelas 8 dapat menyelesaikan tugas Bangun Ruang Sisi Datar Kelas 8 Halaman 134, 135 yang diberikan oleh bapak ibu/guru. Kunci Jawaban MTK Kelas 8 Semester 2.
7. Sebuah aula berbentuk balok dengan ukuran panjang 9 meter, lebar 7 meter dan tingginya 4 mater. Dinding bagian dalamnya akan dicat dengan biaya Rp50.000,00 per meter persegi. Seluruh biaya pengecetan aula adalah ....
A. Rp2.700.000,00
B. Rp6.400.000,00
C. Rp8.200.000,00
D. Rp12.600.000,00
8. Perbandingan panjang,lebar dan tinggi sebuah balok adalah 4:3:2.Jika luas alas balok tersebut adalah 108 cm2,maka hitunglah luas permukaan balok tersebut .
9. Perhatikan gambar kubus di bawah ini. Jika sisi atas dan sisi bawah kubus tersebut dicat dengan warna merah, sedangkan sisi lain dicat dengan warna biru, kemudian kubus dipotongpotong menjadi 64 kubus satuan. Tentukan banyak kubus satuan yang memiliki warna biru saja.
10. Diketahui pada setiap sisi kubus dituliskan sebuah bilangan asli. Setiap titik sudutnya diberi nilai yang merupakan hasil kali dari tiga bilangan pada tiga sisi yang berpotongan di titik sudut tersebut. Jika jumlah semua bilangan pada titik-titik sudut tersebut sama dengan 231, tentukan jumlah semua bilangan yang dituliskan pada sisi-sisi kubus tersebut.
Kunci Jawaban Matematika Kelas 8 Halaman 134, 135 Ayo Kita Berlatih 8.1
6. Diketahui luas suatu jaring" balok adalah 484 cm persegi. bagaimana cara menemukan ukuran balok tersebut?
Jawaban :
Luas jaring-jaring balok = 2 x (pl + pt + lp)
484 = 2 x (pl + pt + lp)
(pl + pt + lp) = 484 / 2
(pl + pt + lt) = 242
karena kita belum mengetahui panjang, lebar, dan tinggi maka kita dapat menggunakan permisalan 2 nilai, contoh : panjang = 1, lebar = 2, selanjutnya kita dapat mencari tingginya dengan mensubtitusikan panjang dan lebar kedalam persamaan diatas.
Misal : p = 1cm , l = 2cm
(pl + pt + lt) = 242
(2 + t + 2t) = 242
3t = 240
t = 80 cm
Sehingga untuk soal ini kita dapat menemukan ukuran balok tersebut dalam banyak jenis ukuran.
Jadi, untuk menemukan ukuran balok dengan luas 484cm persegi, langkah yang harus dilakukan adalah mencari persamaan paling sederhana lalu menentukan 2 nilai dari panjang atau lebar atau tinggi. Untuk mencari nilai yang lainnya kita tinggal mensubtitusikan 2 nilai tersebut ke dalam persamaan.
Luas jaring-jaring balok = 2 x (pl + pt + lp)
484 = 2 x (pl + pt + lp)
(pl + pt + lp) = 484 / 2
(pl + pt + lt) = 242
karena kita belum mengetahui panjang, lebar, dan tinggi maka kita dapat menggunakan permisalan 2 nilai, contoh : panjang = 1, lebar = 2, selanjutnya kita dapat mencari tingginya dengan mensubtitusikan panjang dan lebar kedalam persamaan diatas.
Misal : p = 1cm , l = 2cm
(pl + pt + lt) = 242
(2 + t + 2t) = 242
3t = 240
t = 80 cm
Sehingga untuk soal ini kita dapat menemukan ukuran balok tersebut dalam banyak jenis ukuran.
Jadi, untuk menemukan ukuran balok dengan luas 484cm persegi, langkah yang harus dilakukan adalah mencari persamaan paling sederhana lalu menentukan 2 nilai dari panjang atau lebar atau tinggi. Untuk mencari nilai yang lainnya kita tinggal mensubtitusikan 2 nilai tersebut ke dalam persamaan.
7. Sebuah aula berbentuk balok dengan ukuran panjang 9 meter, lebar 7 meter dan tingginya 4 mater. Dinding bagian dalamnya akan dicat dengan biaya Rp50.000,00 per meter persegi. Seluruh biaya pengecetan aula adalah ....
A. Rp2.700.000,00
B. Rp6.400.000,00
C. Rp8.200.000,00
D. Rp12.600.000,00
Jawaban :
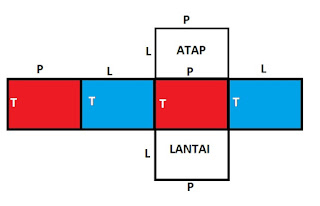
*Perhatikan ilustrasi gambar diatas*
- dari ilustrasi tersebut dapat dilihat bahwa jumlah dinding ada 4 sisi, (atap dan lantai tidak dihitung)
Total luas dinding = 2 x (PT + LT)
= 2 x ( (9x4) + (7x4))
= 2 x (36 + 28)
= 2 x 64
= 128 m2
Total biaya = Total luas dinding x harga permeter persegi
= 128 x 50.000
= Rp.6.400.000,00
Jadi, seluruh biaya pengecetan aula adalah B. Rp.6.400.000,00.
*Perhatikan ilustrasi gambar diatas*
- dari ilustrasi tersebut dapat dilihat bahwa jumlah dinding ada 4 sisi, (atap dan lantai tidak dihitung)
Total luas dinding = 2 x (PT + LT)
= 2 x ( (9x4) + (7x4))
= 2 x (36 + 28)
= 2 x 64
= 128 m2
Total biaya = Total luas dinding x harga permeter persegi
= 128 x 50.000
= Rp.6.400.000,00
Jadi, seluruh biaya pengecetan aula adalah B. Rp.6.400.000,00.
8. Perbandingan panjang,lebar dan tinggi sebuah balok adalah 4:3:2.Jika luas alas balok tersebut adalah 108 cm2,maka hitunglah luas permukaan balok tersebut .
Jawaban :
Perbandingan panjang : lebar : tinggi = 4:3:2
misalkan,
panjang = 4x
lebar = 3x
tinggi = 2x
Luas alas balok = panjang x lebar
108 = 4x x 3x
108 = 12x2
x2 = 108 / 12
x2 = 9
x = √9
x = 3
panjang = 4x = 4 x 3 = 12cm
lebar = 3x = 3 x 3 = 9cm
tinggi = 2x = 2 x 3 = 6cm
Luas permukaan balok = 2 x (pl + pt + lt)
= 2 x ( (12x9) + (12x6) + (9x6))
= 2 x ( 108 + 72 + 54 )
= 2 x 234
= 468 cm2
Jadi, luas permukaan balok tersebut adalah 468 cm2.
Perbandingan panjang : lebar : tinggi = 4:3:2
misalkan,
panjang = 4x
lebar = 3x
tinggi = 2x
Luas alas balok = panjang x lebar
108 = 4x x 3x
108 = 12x2
x2 = 108 / 12
x2 = 9
x = √9
x = 3
panjang = 4x = 4 x 3 = 12cm
lebar = 3x = 3 x 3 = 9cm
tinggi = 2x = 2 x 3 = 6cm
Luas permukaan balok = 2 x (pl + pt + lt)
= 2 x ( (12x9) + (12x6) + (9x6))
= 2 x ( 108 + 72 + 54 )
= 2 x 234
= 468 cm2
Jadi, luas permukaan balok tersebut adalah 468 cm2.
9. Perhatikan gambar kubus di bawah ini. Jika sisi atas dan sisi bawah kubus tersebut dicat dengan warna merah, sedangkan sisi lain dicat dengan warna biru, kemudian kubus dipotongpotong menjadi 64 kubus satuan. Tentukan banyak kubus satuan yang memiliki warna biru saja.
Jawaban :
Perhatikan beberapa informasi khusus berikut :
- terdapat kubus satuan yang tidak berwarna (berada didalam)
- terdapat kubus satuan yang memiliki satu warna ( merah ) atau ( biru )
- terdapat kubus satuan yang memiliki 2 warna (merah dan biru) atau (biru dan biru)
- terdapat kubus satuan yang memiliki 3 warna ( merah dan 2 biru)
Kubus yang berada didalam berjumlah = 2 x 4 = 8
Kubus satuan yang memiliki satu warna ( merah ) = 2 x 4 = 8
Kubus satuan yang memiliki satu warna ( biru ) = 4 x 4 = 16
Kubus satuan yang memiliki 2 warna (merah dan biru) = 2 x 8 = 16
Kubus satuan yang memiliki 2 warna (biru dan biru) = 2 x 4 = 8
Kubus satuan yang memiliki 3 warna ( merah dan 2 biru) = 1 x 8 = 8
Total seluruh kubus satuan adalah 64.
Total kubus satuan yang memiliki warna biru saja = Kubus satuan yang memiliki satu warna + Kubus satuan yang memiliki 2 warna (biru dan biru)
= 16 + 8
= 24
Jadi, banyak kubus satuan yang hanya memiliki warna biru saja adalah 24.
Perhatikan beberapa informasi khusus berikut :
- terdapat kubus satuan yang tidak berwarna (berada didalam)
- terdapat kubus satuan yang memiliki satu warna ( merah ) atau ( biru )
- terdapat kubus satuan yang memiliki 2 warna (merah dan biru) atau (biru dan biru)
- terdapat kubus satuan yang memiliki 3 warna ( merah dan 2 biru)
Kubus yang berada didalam berjumlah = 2 x 4 = 8
Kubus satuan yang memiliki satu warna ( merah ) = 2 x 4 = 8
Kubus satuan yang memiliki satu warna ( biru ) = 4 x 4 = 16
Kubus satuan yang memiliki 2 warna (merah dan biru) = 2 x 8 = 16
Kubus satuan yang memiliki 2 warna (biru dan biru) = 2 x 4 = 8
Kubus satuan yang memiliki 3 warna ( merah dan 2 biru) = 1 x 8 = 8
Total seluruh kubus satuan adalah 64.
Total kubus satuan yang memiliki warna biru saja = Kubus satuan yang memiliki satu warna + Kubus satuan yang memiliki 2 warna (biru dan biru)
= 16 + 8
= 24
Jadi, banyak kubus satuan yang hanya memiliki warna biru saja adalah 24.
Jawaban :
Misalkan bagian sampingnya adalah A,B,C,D dan bagian atap dan alasnya adalah E dan F.
Terdapat 8 titik sudut pada kubus, sehingga berdasarkan soal tersebut maka nilai dari tiap sudutnya adalah
Jumlah total nilai titik sudut = ABE + ABF + BCE + BCF + CDE + CDF + ADE + ADF
231 = E(AB + BC + CD + AD) + F(AB + BC + CD + AD)
231 = (E+F) (AB + BC + CD + AD)
231 = (E+F) (A(B+D) + C(B+D)
231 = (E+F) (A+C) (B+D)
Faktor dari 231 adalah 3 x 7 x 11
Sehingga jumlah semua sisi kubus adalah 3 + 7 + 11 = 21
Jadi, jumlah semua bilangan yang dituliskan pada sisi-sisi kubus teresbut adalah 21.
Misalkan bagian sampingnya adalah A,B,C,D dan bagian atap dan alasnya adalah E dan F.
Terdapat 8 titik sudut pada kubus, sehingga berdasarkan soal tersebut maka nilai dari tiap sudutnya adalah
Jumlah total nilai titik sudut = ABE + ABF + BCE + BCF + CDE + CDF + ADE + ADF
231 = E(AB + BC + CD + AD) + F(AB + BC + CD + AD)
231 = (E+F) (AB + BC + CD + AD)
231 = (E+F) (A(B+D) + C(B+D)
231 = (E+F) (A+C) (B+D)
Faktor dari 231 adalah 3 x 7 x 11
Sehingga jumlah semua sisi kubus adalah 3 + 7 + 11 = 21
Jadi, jumlah semua bilangan yang dituliskan pada sisi-sisi kubus teresbut adalah 21.

Belum ada Komentar untuk "Kunci Jawaban Matematika Kelas 8 Halaman 134, 135 Ayo Kita Berlatih 8.1"
Posting Komentar