Kunci Jawaban Matematika Kelas 7 Halaman 242 Ayo Kita Berlatih 8.4
Berikut ini adalah pembahasan dan Kunci Jawaban Matematika Kelas 7 Semester 2 Halaman 242. Bab 8 Segiempat dan Segitiga Ayo Kita berlatih 8.4 Hal 242 Nomor 1, 2, 3, 4, 5. Kunci jawaban ini dibuat untuk membantu mengerjakan soal matematika bagi kelas 7 di semester 2 halaman 242. Semoga dengan adanya pembahasan serta kunci jawaban ini adik-adik kelas 7 dapat menyelesaikan tugas Segiempat dan Segitiga Matematika Kelas 7 Halaman 242 yang diberikan oleh bapak ibu/guru. Kunci Jawaban MTK Kelas 7 Semester 2.
2. Diketahui layang-layang ABCD mempunyai luas 1.200 cm2. Selain itu, ada layang-layang PQRS yang masing-masing panjang diagonalnya dua kali panjang diagonal-diagonal layang-layang ABCD. Tentukan luas layang-layang PQRS!
3. Diketahui panjang diagonal layang-layang HIJK adalah 8 cm dan 12 cm. Tanpa menggunakan penggaris, buatlah gambar layang-layang HIJK tersebut. Bandingkan hasilnya dengan layang-layang HIJK yang dibuat dengan penggaris!
4. Tiga persegi masing-masing panjang sisinya 6 cm, 10 cm dan 8 cm ditempatkan seperti pada gambar di bawah. Tentukan luas daerah yang diarsir.
5. Bangunan di bawah ini mempunyai empat sisi yang kongruen dan luasnya adalah 132 cm2. Carilah kelilingnya.
Daftar Isi Kunci Jawaban Ayo Kita Berlatih 8.4 :
- Baca Juga : Kunci Jawaban Halaman 242 Nomor 1 - 5
- Baca Juga : Kunci Jawaban Halaman 243 Nomor 6 - 8
- Baca Juga : Kunci Jawaban Halaman 244 Nomor 9 - 15
Kunci Jawaban Matematika Kelas 7 Halaman 242 Ayo Kita Berlatih 8.4
1. Tentukan ukuran diagonal-diagonal suatu belah ketupat yang memiliki luas 48 cm2!
Jawaban :
Sifat-sifat belah ketupat yaitu :
- memiliki 4 sisi yang sama panjang
- memiliki diagonal yang tegag lurus dan sama panjang
Dari sifat belah ketupat tersebut maka,
d1 = d2 = d
Luas belah ketupat = 1/2 x d1 x d2
Luas belah ketupat = 1/2 x d x d
48 = 1/2 x d2
d2 = 48 x 2
d2 = 96
d = √96
= √16 x 6
= 4 √6 cm2
Jadi, ukuruan diagonal-diagonal belah ketupat yang memiliki luas 96 cm2 adalah d1 = 4 √6 cm dan d2 = 4 √6 cm.
Sifat-sifat belah ketupat yaitu :
- memiliki 4 sisi yang sama panjang
- memiliki diagonal yang tegag lurus dan sama panjang
Dari sifat belah ketupat tersebut maka,
d1 = d2 = d
Luas belah ketupat = 1/2 x d1 x d2
Luas belah ketupat = 1/2 x d x d
48 = 1/2 x d2
d2 = 48 x 2
d2 = 96
d = √96
= √16 x 6
= 4 √6 cm2
Jadi, ukuruan diagonal-diagonal belah ketupat yang memiliki luas 96 cm2 adalah d1 = 4 √6 cm dan d2 = 4 √6 cm.
2. Diketahui layang-layang ABCD mempunyai luas 1.200 cm2. Selain itu, ada layang-layang PQRS yang masing-masing panjang diagonalnya dua kali panjang diagonal-diagonal layang-layang ABCD. Tentukan luas layang-layang PQRS!
Jawaban :
Luas layang-layang pertama = 1/2 x d1 x d2
Luas layang-layang kedua = 1/2 x ( 2 x d1 ) x (2 x d2 )
= 1/2 x 2 x 2 x d1 x d2
= 4 x ( 1/2 x d1 x d2 )
= 4 x luas layang-layang pertama
= 4 x 1.200
= 4.800 cm2
Jadi, luas layang-layang PQRS adalah 4.800 cm2.
Luas layang-layang pertama = 1/2 x d1 x d2
Luas layang-layang kedua = 1/2 x ( 2 x d1 ) x (2 x d2 )
= 1/2 x 2 x 2 x d1 x d2
= 4 x ( 1/2 x d1 x d2 )
= 4 x luas layang-layang pertama
= 4 x 1.200
= 4.800 cm2
Jadi, luas layang-layang PQRS adalah 4.800 cm2.
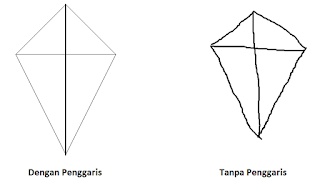
3. Diketahui panjang diagonal layang-layang HIJK adalah 8 cm dan 12 cm. Tanpa menggunakan penggaris, buatlah gambar layang-layang HIJK tersebut. Bandingkan hasilnya dengan layang-layang HIJK yang dibuat dengan penggaris!
Jawaban :
Hasil yang didapat dari menggambar layang-layang tanpa penggaris adalah layang-layang tidak simetris. Ukuran diagonal-diagonal serta sisi-sisi pada layangan tidak sesuai dengan yang ditentukan.
Jadi, dalam menggambar sebuah bangun ruang di sebuah kertas atau buku memerlukan bantuan sebuah penggaris agar hasil yang diinginkan sesuai dengan ketentuan yang diminta.
Jawaban :
*Perhatikan ilustrasi gambar diatas*
- terdapat trapesium ABCD
- terdapat persegi panjang Merah
- Terdapat segitiga Biru
Untuk mencari luas daerah yang diarsir maka langkah yang harus kita lakukan adalah mencari luas trapesium lalu dikurangi dengan luas persegi panjang dan juga luas segitiga.
Luas trapesium ABCD = 1/2 x (6 + 24 ) x 10
= 150 cm2
Luas persegi panjang Merah = panjang x lebar
= 6 x 4
= 24 cm2
Lua segitiga Biru = 1/2 x alas x tinggi
= 1/2 x (6 + 10) x 6
= 48
Luas daerah yang diarsir = luas trapesium ABCD - luas persegi panjang - luas segitiga
= 150 - 24 - 48
= 78 cm2
Jadi, luas daerah yang diarsir adalah 78 cm2.
5. Bangunan di bawah ini mempunyai empat sisi yang kongruen dan luasnya adalah 132 cm2. Carilah kelilingnya.
Jawaban :
*Perhatikan ilustrasi gambar diatas*
- terdapat persegi coklat dengan luas a x a = a2
- terdapat persegi panjang kuning = luas persegi panjang biru = 4/3 a x a = 4/3 a2
Langkah pertama untuk mencari kelilingnya adalah dengan mencari nilai a terlebih dahulu.
Luas seluruhnya = luas persegi coklat + 2 x luas persegi panjang
= a2 + 2 ( 4/3 a2 )
= a2 + 8/3 a2
132 = a2 + 8/3 a2
132 x 3 = 3 x a2 + 8 a2
396 = 11 a2
a2 = 396/11
a2 = 36
a = √36
= 6
Selanjutnya kita menghitung keliling bangun tersebut dalam a. Sehingga akan diperoleh kelilingnya adalah 12a. Subtitusi nilai a kedalam keliling tersebut.
Keliling = 12a
= 12 x 6
= 72 cm
Jadi, keliling bangun tersebut adalah 72 cm.
*Perhatikan ilustrasi gambar diatas*
- terdapat persegi coklat dengan luas a x a = a2
- terdapat persegi panjang kuning = luas persegi panjang biru = 4/3 a x a = 4/3 a2
Langkah pertama untuk mencari kelilingnya adalah dengan mencari nilai a terlebih dahulu.
Luas seluruhnya = luas persegi coklat + 2 x luas persegi panjang
= a2 + 2 ( 4/3 a2 )
= a2 + 8/3 a2
132 = a2 + 8/3 a2
132 x 3 = 3 x a2 + 8 a2
396 = 11 a2
a2 = 396/11
a2 = 36
a = √36
= 6
Selanjutnya kita menghitung keliling bangun tersebut dalam a. Sehingga akan diperoleh kelilingnya adalah 12a. Subtitusi nilai a kedalam keliling tersebut.
Keliling = 12a
= 12 x 6
= 72 cm
Jadi, keliling bangun tersebut adalah 72 cm.





Belum ada Komentar untuk "Kunci Jawaban Matematika Kelas 7 Halaman 242 Ayo Kita Berlatih 8.4"
Posting Komentar